题目内容
已知f(x)=log
(10-ax)其中a为常数,f(3)=-2.
(1)求a值;
(2)若g(x)=
,对任意的实数m,记V(m)为在定义域内g(x)-mx的最大值与最小值的差,求V(m)的最小值.
| 1 |
| 2 |
(1)求a值;
(2)若g(x)=
|
分析:(1)利用题中条件:“f(3)=-2,”得log
(10-3a)=-2,易求得a值;
(2)由(1)得:g(x)=
,进而得到V(m)=
,下面分情况讨论如下:
①若m<0,②若m=0,V(m)=1;③若0<m<1,④若m=1,V(m)=1;⑤若m>1,V(m)=2m-1≥1.最后综合以上得到V(m)的最小值.
| 1 |
| 2 |
(2)由(1)得:g(x)=
|
|
①若m<0,②若m=0,V(m)=1;③若0<m<1,④若m=1,V(m)=1;⑤若m>1,V(m)=2m-1≥1.最后综合以上得到V(m)的最小值.
解答:解:(1)∵f(3)=-2,
∴log
(10-3a)=-2,⇒10-3a=4,
易求得:a=2;
(2)因为a=2,所以得到:g(x)=
进而得到V(m)=
 分情况讨论如下:
分情况讨论如下:
①若m<0,max{g(x)-mx|x∈[1,3]}=2-3m,
min{g(x)-mx|x∈[1,3]}=1-m,V(m)=1-2m>1
②若m=0,V(m)=1
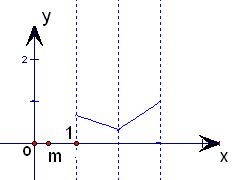
③若0<m<1,如图,g(m)min=V(2)=1-2m,
当0<m≤
,g(m)max=V(3)=2-3m,
当
<m<1,则 g(m)max=V(1)=1-m
此时,分析得V(m)≥
.
④若m=1,V(m)=1.
⑤若m>1,V(m)=2m-1≥1.
综合以上得到V(m)的最小值为
.
∴log
| 1 |
| 2 |
易求得:a=2;
(2)因为a=2,所以得到:g(x)=
|
进而得到V(m)=
|
 分情况讨论如下:
分情况讨论如下:①若m<0,max{g(x)-mx|x∈[1,3]}=2-3m,
min{g(x)-mx|x∈[1,3]}=1-m,V(m)=1-2m>1
②若m=0,V(m)=1
③若0<m<1,如图,g(m)min=V(2)=1-2m,
当0<m≤
| 1 |
| 2 |
当
| 1 |
| 2 |
此时,分析得V(m)≥
| 1 |
| 2 |
④若m=1,V(m)=1.
⑤若m>1,V(m)=2m-1≥1.
综合以上得到V(m)的最小值为
| 1 |
| 2 |
点评:本小题主要考查函数单调性的应用、求对数函数解析式、函数的最值及其几何意义等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目

 (a>0且a≠1).
(a>0且a≠1).