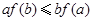题目内容
如图为函数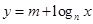 的图象,其中
的图象,其中 、
、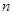 为常数,则下列结论正确( )
为常数,则下列结论正确( )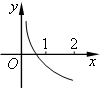
A. , ,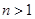 | B. , ,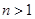 |
C. , , | D. , , |
D
解析试题分析:由图中特殊位置:x=1时函数的值是负值,可得m的取值范围,再根据对数函数的性质即可.解:当x=1时,y=m,由图形,
易知m<0.又∵函数是减函数,∴0<n<1.故选D.答案:D
考点:对数函数图像与性质
点评:本题主要考查知识点:对数与对数函数的图象,属于基础题.

练习册系列答案
相关题目
函数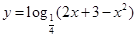 的单调递增区间是( )
的单调递增区间是( )
A.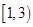 | B.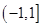 | C.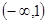 | D. |
若函数 的零点与
的零点与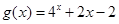 的零点之差的绝对值不超过
的零点之差的绝对值不超过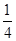 ,则
,则 可以是
可以是
A. =4x-1 =4x-1 | B. =(x-1)2 =(x-1)2 |
C. =ex-2 =ex-2 | D.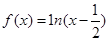 |
若函数f(x)=x3-12x在区间(k-1,k+1)上不是单调函数,则实数k的取值范围是( )
| A.k≤-3或-1≤k≤1或k≥3 | B.-3<k<-1或1<k<3 |
| C.-2<k<2 | D.不存在这样的实数 |
若函数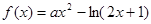 在区间
在区间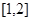 上为单调函数,则实数
上为单调函数,则实数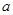 不可能取到的值为
不可能取到的值为
A.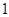 | B.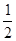 | C.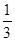 | D.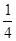 |
下列函数中,在 内为增函数的是( )
内为增函数的是( )
A. | B. |
C. | D. |
已知函数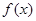 对定义域
对定义域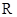 内的任意
内的任意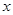 都有
都有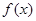 =
=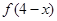 ,且当
,且当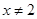 时其导函数
时其导函数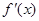 满足
满足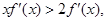 若
若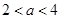 则
则
A.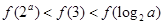 | B.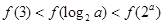 |
C.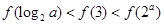 | D.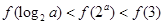 |
 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若 ,则必有( )
,则必有( )