题目内容
将4个相同的小球放人编号为1,2,3的3个盒子中(可以有空盒),当某个盒子中球的个数等于该盒子的编号时称为一个和谐盒,则恰有两个和谐盒的概率为
- A.
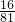
- B.
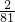
- C.

- D.

D
分析:总的基本事件可分三大类:4小球放入同一个盒中,4个小球放入两个盒中,4个小球放入三个盒中,分别求其个数,可得总数为15,符合条件的有:1号盒放1个,2号盒放2个,3号盒放1个;1号盒放1个,2号盒不放,3号盒放3个,共两种放法,由古典概型的特点可求.
解答:可将4相同小球放入同一个盒中,有3种放法;
将4个相同的小球放入两个盒中,先在3个盒子中任选2个有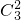 种选法,
种选法,
再用隔板法将4个相同的小球分成有序的两组有3种分法,所以共有9种放法;
将4个相同的小球放入三个盒中,用隔板法将4个相同的小球分成有序的3组有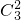 种分法,所以共有3种放法,
种分法,所以共有3种放法,
故共有3+9+3=15种放法.
恰有两个和谐盒的放法有:1号盒放1个,2号盒放2个,3号盒放1个;1号盒放1个,2号盒不放,3号盒放3个,
共两种放法.由古典概型可知:恰有两个和谐盒的概率为:
故选D
点评:本题为古典概型的求解,求对基本事件的数目是解决问题的关键,属基础题.
分析:总的基本事件可分三大类:4小球放入同一个盒中,4个小球放入两个盒中,4个小球放入三个盒中,分别求其个数,可得总数为15,符合条件的有:1号盒放1个,2号盒放2个,3号盒放1个;1号盒放1个,2号盒不放,3号盒放3个,共两种放法,由古典概型的特点可求.
解答:可将4相同小球放入同一个盒中,有3种放法;
将4个相同的小球放入两个盒中,先在3个盒子中任选2个有
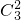 种选法,
种选法,再用隔板法将4个相同的小球分成有序的两组有3种分法,所以共有9种放法;
将4个相同的小球放入三个盒中,用隔板法将4个相同的小球分成有序的3组有
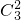 种分法,所以共有3种放法,
种分法,所以共有3种放法,故共有3+9+3=15种放法.
恰有两个和谐盒的放法有:1号盒放1个,2号盒放2个,3号盒放1个;1号盒放1个,2号盒不放,3号盒放3个,
共两种放法.由古典概型可知:恰有两个和谐盒的概率为:

故选D
点评:本题为古典概型的求解,求对基本事件的数目是解决问题的关键,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目







