题目内容

已知x，y∈R，3x²+y²≤3，则2x+3y的最大值是________．

$\text{[math]}$
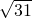
分析：设z=2x+3y得y= $\text{[math]}$ （z-2x），将此代入题中不等式，将不等式化成关于x的一元二次不等式（其中z是参数），根据不等式解集非空，运用根的判别式解关于z的不等式，即可得到z=2x+3y的最大值．
解答：设z=2x+3y，得y= $\text{[math]}$ （z-2x）
代入3x²+y²≤3，得3x²+ $\text{[math]}$ （z-2x）²≤3
化简整理，得 $\text{[math]}$ x²- $\text{[math]}$ zx+ $\text{[math]}$ z²-3≤0
要使以上不等式解集不是空集，则
△=（- $\text{[math]}$ z）²-4× $\text{[math]}$ （ $\text{[math]}$ z²-3）≥0
解之得：z²≤31，可得- $\text{[math]}$ ≤z≤ $\text{[math]}$
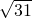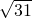
∴z=2x+3y的最大值是 $\text{[math]}$
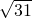
故答案为： $\text{[math]}$
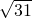
点评：本题给出关于x、y的不等式，求z=2x+3y的最大值．着重考查了一元二次不等式的解集和简单线性规划的应用等知识，属于基础题．

练习册系列答案

优能英语完形填空与阅读理解系列答案

初中英语阅读教程系列答案

领军中考系列答案

名师面对面中考满分策略系列答案

决战中考系列答案

新题型题库系列答案

中考复习与指导系列答案

世纪金榜金榜大讲堂系列答案

经纶学典中考档案系列答案

优倍伴学总复习系列答案

相关题目

已知x，y∈R，且3^x+5^y≥3^-y+5^-x，则x与y一定满足（　　）

（1）已知x＞0，y＞0，且

=2，求x+y的最小值．
（2）已知x，y∈R⁺，且满足

=1，求xy的最大值．
（3）若对任意x＜1，

≤a恒成立，求a的取值范围．

下列说法：
①x＞2是x²-3x+2＞0的充分不必要条件．
②函数y=

图象的对称中心是（1，1）．
③已知x，y∈R，i为虚数单位，且（x-2）i-y=1+i，则（1+i）^x-y的值为-4．
④若函数f(x)=

(3a-1)x+4a(x＜1)

，对任意的x₁≠x₂都有

＜0，则实数a的取值范围是(

，1)．
其中正确命题的序号为

已知x，y∈R⁺，M=

，则M，N，P的大小关系（　　）

已知x，y∈R，且

的最大值是（　　）