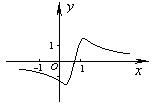题目内容
 (本题12分)已知函数
(本题12分)已知函数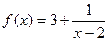 ,
,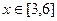 .
.(1)试判断函数
 的单调性,并用定义加以证明;
的单调性,并用定义加以证明; (2)求函数
(2)求函数 的最大值和最小值.
的最大值和最小值.(1) 函数 在
在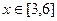 时为减函数, 证明:设
时为减函数, 证明:设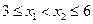 ,
,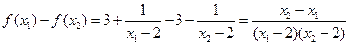 ,
,
显然有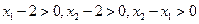 ,故
,故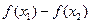
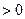 ,从
,从 而函数
而函数 在
在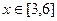 时为减函数
时为减函数
(2) 的最大
的最大 值为
值为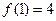 ,
, 的最小值为
的最小值为
 在
在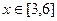 时为减函数, 证明:设
时为减函数, 证明:设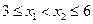 ,
,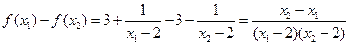 ,
,显然有
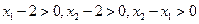 ,故
,故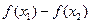
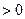 ,从
,从 而函数
而函数 在
在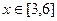 时为减函数
时为减函数(2)
 的最大
的最大 值为
值为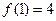 ,
, 的最小值为
的最小值为
解:已知函数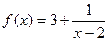 ,
,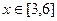 .
.
(1)函数 在
在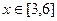 时为减函数。
时为减函数。
证明:设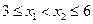 ,
,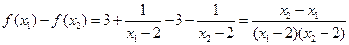 ,
,
显然有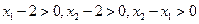 ,故
,故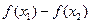
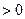 ,从
,从 而函数
而函数 在
在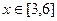 时为减函数。
时为减函数。
(2)由函数 的单调性知:
的单调性知: 的最大
的最大 值为
值为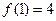 ,
, 的最小值为
的最小值为 .
.
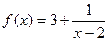 ,
,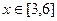 .
.(1)函数
 在
在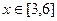 时为减函数。
时为减函数。证明:设
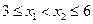 ,
,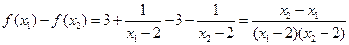 ,
,显然有
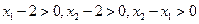 ,故
,故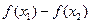
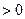 ,从
,从 而函数
而函数 在
在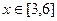 时为减函数。
时为减函数。(2)由函数
 的单调性知:
的单调性知: 的最大
的最大 值为
值为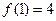 ,
, 的最小值为
的最小值为 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,函数
,函数 .
. 的单调递减区间;
的单调递减区间; 在区间
在区间 上有极值,求
上有极值,求 的取值范围;
的取值范围;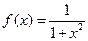 ,试判断函数
,试判断函数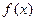 在(0,+∞)上的单调性,并加以证明。
在(0,+∞)上的单调性,并加以证明。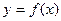 的值域为
的值域为 ,则函数
,则函数 的值域为( )
的值域为( )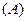
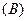
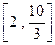
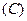
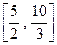
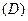
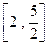
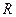 为的函数
为的函数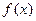 对任意
对任意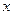 都有
都有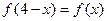 ,若当
,若当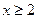 时,
时,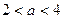 时,有( )
时,有( )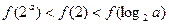
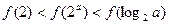
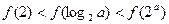
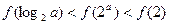
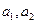 满足
满足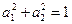 ,那么
,那么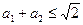 。”
。”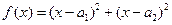 ,因为对一切实数
,因为对一切实数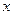 ,恒有
,恒有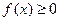 ,
,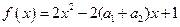 ,从而得
,从而得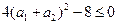 ,所以
,所以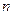 个正实数满足
个正实数满足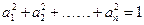 时,你可以构造函数
时,你可以构造函数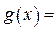 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).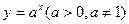 在
在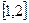 上最大值比最小值大
上最大值比最小值大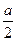 ,则
,则
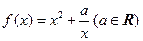 ,则下列结论正确的是( )
,则下列结论正确的是( )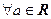 ,
,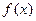 在
在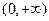 上是增函数
上是增函数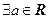 ,
,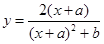 的图象如右图所示,则 (D)
的图象如右图所示,则 (D)