题目内容
9．过点（-2，6）作圆x2+（y-2）2=4的两条切线，切点分别为A，B，则直线AB的方程为x-2y+6=0．分析 求出以（-2，6）、C（0，2）为直径的圆的方程，将两圆的方程相减可得公共弦AB的方程．
解答 解：圆x2+（y-2）2=4的圆心为C（0，2），半径为2，
以（-2，6）、C（0，2）为直径的圆的方程为（x+1）2+（y-4）2=5，
将两圆的方程相减可得公共弦AB的方程x-2y+6=0，
故答案为：x-2y+6=0．
点评 本题考查直线和圆的位置关系以及圆和圆的位置关系、圆的切线性质，体现了数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
19．下列函数中既是轴对称又是增函数的是（ ）
| A． | y=-$\frac{2}{x}$ | B． | y=2x | C． | y=log2x | D． | y=2x |
4．已知实数x，y满足约束条件$\left\{\begin{array}{l}x-y+4≥0\\ x+y≥0\\ y≤4\end{array}\right.$，则目标函数z=x-2y的最小值是（ ）
| A． | 0 | B． | -6 | C． | -8 | D． | -12 |
14．一个几何体的三视图如图所示，则这个几何体的外接球的表面积为 （ ）
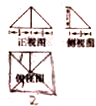
| A． | $\frac{4π}{3}$ | B． | $\frac{8π}{3}$ | C． | 4π | D． | 2π |
1．若l，m，n是不相同的空间直线，α，β是不重合的平面，则下列命题正确的是（ ）
| A． | α∥β，l?α，n?β⇒l∥n?????? | B． | l⊥n，m⊥n⇒l∥m | ||
| C． | l⊥α，l∥β⇒α⊥β | D． | α⊥β，l?α⇒l⊥β |