题目内容
若函数f (x) = x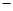
 在[1,+∞)上是增函数,则实数p的取值范围是( )
在[1,+∞)上是增函数,则实数p的取值范围是( )
A. | B. | C. | D. |
A
解析试题分析:因为函数f (x) = x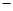
 在[1,+∞)上是增函数,那么可知其导数f‘(x) = 1
在[1,+∞)上是增函数,那么可知其导数f‘(x) = 1
 >0恒成立,则说明了
>0恒成立,则说明了 ,即可故答案为A
,即可故答案为A
考点:本试题考查了函数单调性的运用。
点评:解决函数单调性的关键是对于含有参数的函数能利用定义法或者导数的思想来判定。导数满足的是在给定区间上导数恒大于等于零,来得到参数满足的不等式,进而分离参数求解得到最值。属于中档题。

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
已知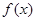 在
在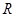 上是减函数,则满足
上是减函数,则满足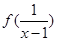 >
> 的实数
的实数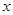 的取值范围是( ).
的取值范围是( ).
| A.(-∞,1) | B.(2,+∞) |
| C.(-∞,1)∪(2,+∞) | D.(1,2) |
函数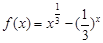 的零点个数为
的零点个数为
| A.0 | B.1 |
| C.2 | D.3 |
函数y= 的定义域为( )
的定义域为( )
A.(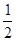 ,+∞) ,+∞) | B.[1,+∞ | C.( 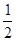 ,1 ,1 | D.(-∞,1)) |
函数 在区间
在区间 单调递增,则实数
单调递增,则实数 的取值范围为
的取值范围为
A. | B. | C. | D. |
若 ,则
,则 ( )
( )
| A.2 | B.4 | C. | D.10 |
函数 的零点一定位于的区间是 ( )
的零点一定位于的区间是 ( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
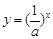 与
与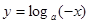 (其中
(其中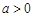 且
且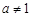 )的图象只可能是( )
)的图象只可能是( )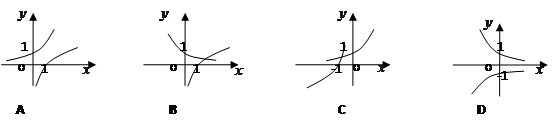
 ,若存在常数C,对任意的
,若存在常数C,对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知 ,则函数
,则函数 在
在 上的几何平均数为( )
上的几何平均数为( ) B.
B. C.
C. D.
D.