题目内容
设函数f(x)=cos(2x+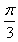 )+sin2x,
)+sin2x,
(1)求函数f(x)的最大值和最小正周期;
(2)设A,B,C为△ABC的三个内角,若cosB=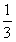 ,
,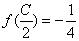 ,且C为锐角,求sinA。
,且C为锐角,求sinA。
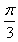 )+sin2x,
)+sin2x, (1)求函数f(x)的最大值和最小正周期;
(2)设A,B,C为△ABC的三个内角,若cosB=
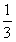 ,
,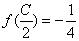 ,且C为锐角,求sinA。
,且C为锐角,求sinA。 解:(1)f(x)=cos(2x+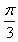 )+sin2x=
)+sin2x=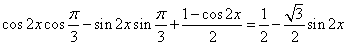 ,
,
所以函数f(x)的最大值为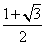 ,最小正周期π;
,最小正周期π;
(2)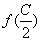
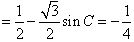 ,所以
,所以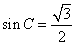 ,
,
因为C为锐角,所以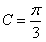 ,
,
又因为在△ABC中,cosB=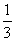 ,所以
,所以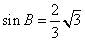 ,
,
所以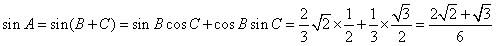 。
。
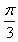 )+sin2x=
)+sin2x=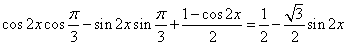 ,
,所以函数f(x)的最大值为
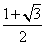 ,最小正周期π;
,最小正周期π;(2)
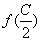
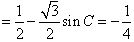 ,所以
,所以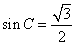 ,
,因为C为锐角,所以
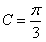 ,
,又因为在△ABC中,cosB=
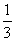 ,所以
,所以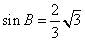 ,
,所以
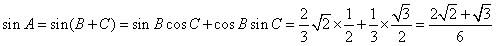 。
。
练习册系列答案
相关题目