题目内容
设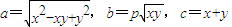 ,若对任意的正实数x,y,都存在以a,b,c为三边长的三角形,则实数p的取值范围是 .
,若对任意的正实数x,y,都存在以a,b,c为三边长的三角形,则实数p的取值范围是 .
【答案】分析:由基本不等式可得a≥ ,c≥2
,c≥2 ,再由三角形任意两边之和大于第三边可得,
,再由三角形任意两边之和大于第三边可得, +2
+2 >
> ,且
,且  +
+ >2
>2 ,且
,且  +2
+2 >
> ,由此求得实数p的取值范围.
,由此求得实数p的取值范围.
解答:解:对于正实数x,y,由于 ≥
≥ =
= ,c=x+y≥2
,c=x+y≥2 ,
, ,且三角形任意两边之和大于第三边,
,且三角形任意两边之和大于第三边,
∴ +2
+2 >
> ,且
,且  +
+ >2
>2 ,且
,且  +2
+2 >
> .
.
解得 1<p<3,故实数p的取值范围是(1,3),
故答案为 (1,3).
点评:本题主要考查基本不等式的应用,注意不等式的使用条件,以及三角形中任意两边之和大于第三边,属于中档题.
 ,c≥2
,c≥2 ,再由三角形任意两边之和大于第三边可得,
,再由三角形任意两边之和大于第三边可得, +2
+2 >
> ,且
,且  +
+ >2
>2 ,且
,且  +2
+2 >
> ,由此求得实数p的取值范围.
,由此求得实数p的取值范围.解答:解:对于正实数x,y,由于
 ≥
≥ =
= ,c=x+y≥2
,c=x+y≥2 ,
, ,且三角形任意两边之和大于第三边,
,且三角形任意两边之和大于第三边,∴
 +2
+2 >
> ,且
,且  +
+ >2
>2 ,且
,且  +2
+2 >
> .
.解得 1<p<3,故实数p的取值范围是(1,3),
故答案为 (1,3).
点评:本题主要考查基本不等式的应用,注意不等式的使用条件,以及三角形中任意两边之和大于第三边,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
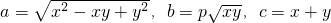 ,若对任意的正实数x,y,都存在以a,b,c为三边长的三角形,则实数p的取值范围是________.
,若对任意的正实数x,y,都存在以a,b,c为三边长的三角形,则实数p的取值范围是________.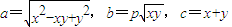 ,若对任意的正实数x,y,都存在以a,b,c为三边长的三角形,则实数p的取值范围是 .
,若对任意的正实数x,y,都存在以a,b,c为三边长的三角形,则实数p的取值范围是 .