题目内容
已知椭圆 +
+ =1(a>b>0)与双曲线
=1(a>b>0)与双曲线 -
- =1有相同的焦点,则椭圆的离心率为
=1有相同的焦点,则椭圆的离心率为
- A.

- B.

- C.

- D.

D
分析:根据椭圆与双曲线有相同的焦点,结合它们的方程得出关于a,b的等式,找到a=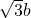 ,再根据这个关系得到椭圆的长半轴m=
,再根据这个关系得到椭圆的长半轴m= a=
a= b,而短半轴n=
b,而短半轴n= b,从而得到c用b表示的关系式,用离心率的公式可得到此椭圆的离心率.
b,从而得到c用b表示的关系式,用离心率的公式可得到此椭圆的离心率.
解答:∵椭圆方程为 +
+ =1(a>b>0)
=1(a>b>0)
∴椭圆焦点坐标为F(±c,0)
其中c满足:c2=2a2-2b2…①
又∵双曲线方程为 -
- =1且与已知椭圆有相同的焦点
=1且与已知椭圆有相同的焦点
∴双曲线焦点坐标也为F(±c,0),
满足c2=a2+b2…②.
对照①②,得2a2-2b2=a2+b2,
∴a2=3b2?a=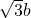 ,
,
可得椭圆的长半轴m= a=
a= b
b
短半轴n= b
b
∴半焦距c= =2b
=2b
离心率e=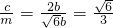 ,
,
即则椭圆的离心率为 .
.
故选D.
点评:本小题考查双曲线与椭圆的关系,考查圆锥曲线的基本元素之间的关系问题,同时双曲线、椭圆的相应知识也进行了综合性考查.
分析:根据椭圆与双曲线有相同的焦点,结合它们的方程得出关于a,b的等式,找到a=
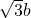 ,再根据这个关系得到椭圆的长半轴m=
,再根据这个关系得到椭圆的长半轴m= a=
a= b,而短半轴n=
b,而短半轴n= b,从而得到c用b表示的关系式,用离心率的公式可得到此椭圆的离心率.
b,从而得到c用b表示的关系式,用离心率的公式可得到此椭圆的离心率.解答:∵椭圆方程为
 +
+ =1(a>b>0)
=1(a>b>0)∴椭圆焦点坐标为F(±c,0)
其中c满足:c2=2a2-2b2…①
又∵双曲线方程为
 -
- =1且与已知椭圆有相同的焦点
=1且与已知椭圆有相同的焦点∴双曲线焦点坐标也为F(±c,0),
满足c2=a2+b2…②.
对照①②,得2a2-2b2=a2+b2,
∴a2=3b2?a=
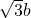 ,
,可得椭圆的长半轴m=
 a=
a= b
b短半轴n=
 b
b∴半焦距c=
 =2b
=2b离心率e=
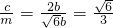 ,
,即则椭圆的离心率为
 .
.故选D.
点评:本小题考查双曲线与椭圆的关系,考查圆锥曲线的基本元素之间的关系问题,同时双曲线、椭圆的相应知识也进行了综合性考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则椭圆方程为( )
,则椭圆方程为( ) +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则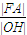 的最大值为 .
的最大值为 . +
+ =1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则
=1(a>b>0)的中心为O,右焦点为F、右顶点为A,右准线与x轴的交点为H,则 的最大值为 .
的最大值为 . =1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若
=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若 (应为PB),则离心率为
(应为PB),则离心率为 B、
B、 C、
C、 D、
D、