题目内容
下列函数![]() 中,满足“对任意的
中,满足“对任意的![]() ,当
,当![]() 时,总有
时,总有![]() ”的是( )
”的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【解析】本题考查了函数单调性的定义,以及基本初等函数的单调,即反比例函数、二次函数、指数函数和对数函数单调性的应用.∵对任意x1、x2∈![]() ,当x1<x2时,都有f(x1)>f(x2),∴函数在
,当x1<x2时,都有f(x1)>f(x2),∴函数在![]() 上是减函数;A、由于
上是减函数;A、由于![]() ,由二次函数的性质知,在
,由二次函数的性质知,在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,故A不对; B、根据对数的真数大于零得函数的定义域为
上是增函数,故A不对; B、根据对数的真数大于零得函数的定义域为![]() ,故B不对; C、由反比例函数的性质知,此函数函数在
,故B不对; C、由反比例函数的性质知,此函数函数在![]() 上是减函数,故C正确; D、由于e>1,则由指数函数的单调性知,在
上是减函数,故C正确; D、由于e>1,则由指数函数的单调性知,在![]() 上是增函数,故D不对;故选C.
上是增函数,故D不对;故选C.

练习册系列答案
相关题目
 中,满足“对任意
中,满足“对任意 ,
,
 (0,
(0, ),当
),当 >
> 的是(
)
的是(
)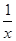 B.
B.
 C .
C . D.
D.