Question

在平面直角坐标系xOy中，已知三点A(-1，0)，B(1，0)，C(-1，)，以A、B为焦点的椭圆经过点C.

(Ⅰ)求椭圆的方程；

(Ⅱ)设点D(0，1)，是否存在不平行于x轴的直线l与椭圆交于不同两点M、N，使()·=0?若存在，求出直线l斜率的取值范围；若不存在，请说明理由；

(Ⅲ)若对于y轴上的点P(0，n)(n≠0)，存在不平行于x轴的直线l与椭圆交于不同两点M、N，使(+)·=0，试求n的取值范围.

Answer 1

解:(Ⅰ)设椭圆方程为(a＞b＞0),

据A(-l,0),B(1,0),C(-1,)知,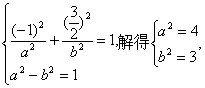

∴所求椭圆方程为=1.

(Ⅱ)∵条件(等价于,

∴若存在符合条件的直线,该直线的斜率一定存在,否则与点D(0,1)不在x轴上矛盾.∴可设直线l:y=kx+m(k≠0)由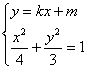,得(3+4k²)x²+8kmx+4m²-12=0,

由△=64k²m²-4(3+4k²)(4m²-12)＞0,得4k²+3＞m²,  

设M(x₁,y₁),N(x₂,y₂),MN的中点为Q(x₀,y₀),

则x₀=

又∵∴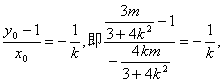解得:m=-3-4k².   

(将点的坐标代入亦可得到此结果)

由4k²+3＞m²得,4k²+3＞(3+4k²)²  得,4k²＜-2,这是不可能的.

故满足条件的直线不存在.  (10分)

(Ⅲ)据(Ⅱ)有,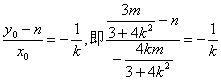

解得,m=-n(3+4k²),

由4k²+3＞m²得4k²+3＞n²(3+4k²)²,即4k²＜-3,要使k存在,只需-3＞0(n≠0),

∴n的取值范围是(-,0)∪(0,).