题目内容
已知数列{an}的前n项和为Sn,且满足Sn=1-an(n∈N*).各项为正数的数列{bn}中,对于一切n∈N*,有
 ,且b1=1,b2=2,b3=3.
,且b1=1,b2=2,b3=3.(1)求数列{an}和{bn}的通项公式;
(2)设数列{anbn}的前n项和为Tn,求证:Tn<2.
【答案】分析:(1)由Sn=1-an,解得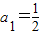 .an=Sn-Sn-1=(1-an)-(1-an-1),由此得2an=an-1,从而得到数列{an}的通项公式.对于一切n∈N*,有
.an=Sn-Sn-1=(1-an)-(1-an-1),由此得2an=an-1,从而得到数列{an}的通项公式.对于一切n∈N*,有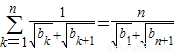 ,当n≥2时,有
,当n≥2时,有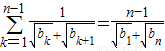 ,由此得(n-1)bn+1-nbn+b1=0,从而得到数列{bn}的通项公式.
,由此得(n-1)bn+1-nbn+b1=0,从而得到数列{bn}的通项公式.
(2)由数列anbn的前n项和为Tn,知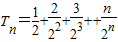 ,再由错位相减法知
,再由错位相减法知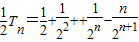 =
=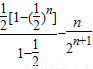 =
=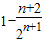 .由此能够证明Tn<2.
.由此能够证明Tn<2.
解答:(1)解:∵Sn=1-an,
当n=1时,a1=S1=1-a1,解得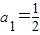 .(1分)
.(1分)
当n≥2时,an=Sn-Sn-1=(1-an)-(1-an-1),
得2an=an-1,即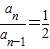 .(3分)
.(3分)
∴数列an是首项为 ,公比为
,公比为 的等比数列.
的等比数列.
∴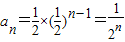 .(4分)
.(4分)
∵对于一切n∈N*,有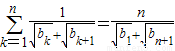 ,①
,①
当n≥2时,有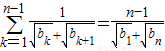 ,②
,②
1-2②得: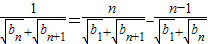 3
3
化简得:(n-1)bn+1-nbn+b1=0,③
用n+1替换③式中的n,得:nbn+2-(n+1)bn+1+b1=0,④(6分)
③-④整理得:bn+2-bn+1=bn+1-bn,
∴当n≥2时,数列bn为等差数列.
∵b3-b2=b2-b1=1,
∴数列bn为等差数列.(8分)
∵b1=1,b2=2
∴数列bn的公差d=1.
∴bn=1+(n-1)=n.(10分)
(2)证明:∵数列anbn的前n项和为Tn,
∴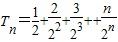 ,⑤
,⑤
∴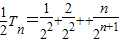 ,⑥
,⑥
⑤-⑥得: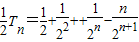 (12分)=
(12分)=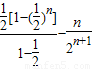 =
=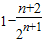 .
.
∴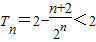 .(14分)
.(14分)
点评:本题考查等差数列和等比数列的通项公式的求法和数列前n项和的证明,解题时要熟练掌握数列的性质和应用,注意错位相减法的灵活运用.
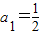 .an=Sn-Sn-1=(1-an)-(1-an-1),由此得2an=an-1,从而得到数列{an}的通项公式.对于一切n∈N*,有
.an=Sn-Sn-1=(1-an)-(1-an-1),由此得2an=an-1,从而得到数列{an}的通项公式.对于一切n∈N*,有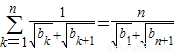 ,当n≥2时,有
,当n≥2时,有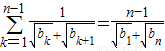 ,由此得(n-1)bn+1-nbn+b1=0,从而得到数列{bn}的通项公式.
,由此得(n-1)bn+1-nbn+b1=0,从而得到数列{bn}的通项公式.(2)由数列anbn的前n项和为Tn,知
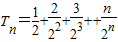 ,再由错位相减法知
,再由错位相减法知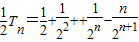 =
=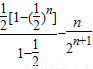 =
=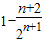 .由此能够证明Tn<2.
.由此能够证明Tn<2.解答:(1)解:∵Sn=1-an,
当n=1时,a1=S1=1-a1,解得
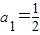 .(1分)
.(1分)当n≥2时,an=Sn-Sn-1=(1-an)-(1-an-1),
得2an=an-1,即
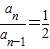 .(3分)
.(3分)∴数列an是首项为
 ,公比为
,公比为 的等比数列.
的等比数列.∴
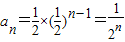 .(4分)
.(4分)∵对于一切n∈N*,有
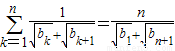 ,①
,①当n≥2时,有
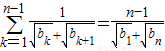 ,②
,②1-2②得:
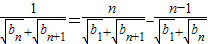 3
3化简得:(n-1)bn+1-nbn+b1=0,③
用n+1替换③式中的n,得:nbn+2-(n+1)bn+1+b1=0,④(6分)
③-④整理得:bn+2-bn+1=bn+1-bn,
∴当n≥2时,数列bn为等差数列.
∵b3-b2=b2-b1=1,
∴数列bn为等差数列.(8分)
∵b1=1,b2=2
∴数列bn的公差d=1.
∴bn=1+(n-1)=n.(10分)
(2)证明:∵数列anbn的前n项和为Tn,
∴
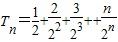 ,⑤
,⑤∴
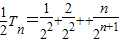 ,⑥
,⑥⑤-⑥得:
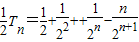 (12分)=
(12分)=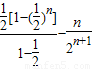 =
=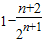 .
.∴
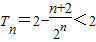 .(14分)
.(14分)点评:本题考查等差数列和等比数列的通项公式的求法和数列前n项和的证明,解题时要熟练掌握数列的性质和应用,注意错位相减法的灵活运用.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |