题目内容
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,半焦距为
,半焦距为![]() ,离心率
,离心率![]() ,又直线
,又直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 中点.
中点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求弦
,求弦![]() 的长;
的长;
(3)若点![]() 恰好平分弦
恰好平分弦![]() ,求实数
,求实数![]() ;
;
(4)若满足![]() ,求实数
,求实数![]() 的取值范围并求
的取值范围并求![]() 的值;
的值;
(5)设圆![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() 与点
与点![]() ,求
,求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
(6)若直线![]() 是圆
是圆![]() 的切线,证明
的切线,证明![]() 的大小为定值.
的大小为定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
, ![]() ;(4)
;(4)![]() ,
,![]() ;(5)
;(5)![]() ;(6)见解析.
;(6)见解析.
【解析】试题分析:(1)根据题意得方程组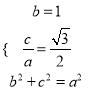 ,解出方程组得椭圆方程;(2)联立方程组,解出即可得交点坐标,进而得弦长;(3)利用“点差法”可得斜率
,解出方程组得椭圆方程;(2)联立方程组,解出即可得交点坐标,进而得弦长;(3)利用“点差法”可得斜率![]() ,根据点
,根据点![]() 在直线上故而可得
在直线上故而可得![]() 的值;(4)在(3)式的基础上等号两边同时除以
的值;(4)在(3)式的基础上等号两边同时除以![]() ,即可得
,即可得![]() 的值,联立直线与椭圆的方程,根据
的值,联立直线与椭圆的方程,根据![]() 可得
可得![]() ,结合韦达定理可得
,结合韦达定理可得![]() 点坐标,根据
点坐标,根据![]() ,所以
,所以![]() ,化简可得
,化简可得![]() ,两者结合即可得结果;(5)根据点
,两者结合即可得结果;(5)根据点![]() 与点
与点![]() 关于
关于![]() 轴对称,设出
轴对称,设出![]() 的坐标,再利用点在椭圆上,利用数量积的坐标表达式得出
的坐标,再利用点在椭圆上,利用数量积的坐标表达式得出![]() 的表达式,最后利用二次函数的性质求其最小值及求此时圆的方程;(6)利用(4)中的结果结合韦达定理可得
的表达式,最后利用二次函数的性质求其最小值及求此时圆的方程;(6)利用(4)中的结果结合韦达定理可得![]() ,根据直线与圆相切可得
,根据直线与圆相切可得![]() ,故而
,故而![]() ,即可得结果.
,即可得结果.
试题解析:(1)根据题意:  ,解得
,解得![]() ,所以椭圆
,所以椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)联立直线方程和椭圆方程: 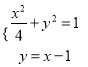 ,整理得:
,整理得: ![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() ,
, ![]() ,则
,则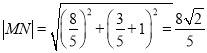 .
.
(3)![]() 恰好平分弦
恰好平分弦![]() ,所以
,所以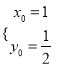 ,
,
![]() 在椭圆上,则
在椭圆上,则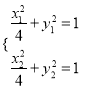 ,上下相减得
,上下相减得![]() ,
,
即![]() ,即
,即![]() ,则
,则![]() ,即
,即![]() ,
,
点![]() 在直线上,所以直线
在直线上,所以直线![]() ,整理得
,整理得![]() ,所以
,所以![]() ,
,
综上所述: ![]() ,
, ![]() .
.
(4)由(3)知![]() ,等号两边同时除以
,等号两边同时除以![]() ,
,
得![]() ,所以
,所以![]() .
.
联立直线方程和椭圆方程: 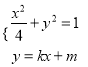 ,整理得:
,整理得: ![]() ,
,
![]() ,解得
,解得![]() ,
,
则![]() ,所以
,所以![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,则
,则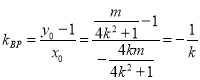 ,化简得
,化简得![]() ,则
,则![]() ,又
,又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
综上所述: ![]() ,
,![]() .
.
(5)设![]() ,
, ![]() ,则
,则![]()
![]() ,
,
所以![]() ,点
,点![]() 与点
与点![]() 在椭圆上:
在椭圆上: ![]() ,所以
,所以![]() ,当
,当![]() 时,
时, ![]() 取得最小值
取得最小值![]() ,此时
,此时![]() ,
, ![]() ,
,
综上所述: ![]() 的最小值为
的最小值为![]() ,此时圆
,此时圆![]() 的方程
的方程![]() .
.
(6)由(4)得![]() 且
且![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]()
直线![]() 是圆
是圆![]() 的切线,所以点
的切线,所以点![]() 到直线
到直线![]() 距离为
距离为![]() ,
,
即![]() ,整理得
,整理得![]() ,所以
,所以![]() ,即
,即![]() 的大小为
的大小为![]() .
.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】假设关于某设备的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
若由资料知, ![]() 对
对![]() 呈线性相关关系,试求:
呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
参考公式:回归直线方程: ![]() .其中
.其中
(注: ![]() )
)
