题目内容
函数y=cos2x+2cosx,x∈(0,π)的单调递增区间为
- A.
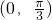
- B.
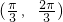
- C.
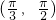
- D.
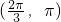
D
分析:把函数解析式的第一项利用二倍角的余弦函数公式化简,得到y与cosx成二次函数关系,找出此二次函数的对称轴,找出二次函数的减区间,同时找出余弦函数减区间,根据复合函数的增减性可得原函数为增函数,求出此时x的范围,即为函数的单调递增区间.
解答:y=cos2x+2cosx
=2cos2x+2cosx-1,
此时y与cosx成的是二次函数关系,
其图象为开口向上的抛物线,对称轴为cosx=- ,
,
当cosx∈(-1,- )时,余弦函数cosx为减函数,二次函数也为减函数,原函数为增函数,
)时,余弦函数cosx为减函数,二次函数也为减函数,原函数为增函数,
∵x∈(0,π),
∴此时x∈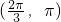 ,即为函数的递增区间.
,即为函数的递增区间.
故选D
点评:此题考查了二倍角的余弦函数公式,二次函数的性质,复合函数的单调性,以及余弦函数的定义域和值域,利用二倍角的余弦函数公式化简函数解析式是本题的突破点.
分析:把函数解析式的第一项利用二倍角的余弦函数公式化简,得到y与cosx成二次函数关系,找出此二次函数的对称轴,找出二次函数的减区间,同时找出余弦函数减区间,根据复合函数的增减性可得原函数为增函数,求出此时x的范围,即为函数的单调递增区间.
解答:y=cos2x+2cosx
=2cos2x+2cosx-1,
此时y与cosx成的是二次函数关系,
其图象为开口向上的抛物线,对称轴为cosx=-
 ,
,当cosx∈(-1,-
 )时,余弦函数cosx为减函数,二次函数也为减函数,原函数为增函数,
)时,余弦函数cosx为减函数,二次函数也为减函数,原函数为增函数,∵x∈(0,π),
∴此时x∈
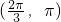 ,即为函数的递增区间.
,即为函数的递增区间.故选D
点评:此题考查了二倍角的余弦函数公式,二次函数的性质,复合函数的单调性,以及余弦函数的定义域和值域,利用二倍角的余弦函数公式化简函数解析式是本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了得到函数y=sin(2x-
)的图象,可以将函数y=cos2x的图象( )
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|