题目内容
已知函数 ,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是
,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是
- A.

- B.(1,2)
- C.
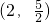
- D.(0,2)
C
分析:先作出函数的图象,结合图象先判断a,b,c的取值范围和对应关系.然后去判断abc的取值范围.
解答: 解:先作出函数f(x)的图象如图:
解:先作出函数f(x)的图象如图:
因为a,b,c大小不相等,不妨设a<b<c.由-2x+5=0,解得x= .因为f(a)=f(b)=f(c),
.因为f(a)=f(b)=f(c),
所以由图象可知,0<a<1,1<b<2,2<c< .由.f(a)=f(b),
.由.f(a)=f(b),
得 ,即
,即 ,所以
,所以 ,
,
解得ab=1.所以abc=c∈(2, ),所以abc的取值范围是(2,
),所以abc的取值范围是(2, ),选C.
),选C.
故选C.
点评:本题考查函数对数函数的图象与性质,以及根据函数与方程的关系求参数的取值范围问题.利用数形结合思想是解决这类问题的关键.
分析:先作出函数的图象,结合图象先判断a,b,c的取值范围和对应关系.然后去判断abc的取值范围.
解答:
 解:先作出函数f(x)的图象如图:
解:先作出函数f(x)的图象如图:因为a,b,c大小不相等,不妨设a<b<c.由-2x+5=0,解得x=
 .因为f(a)=f(b)=f(c),
.因为f(a)=f(b)=f(c),所以由图象可知,0<a<1,1<b<2,2<c<
 .由.f(a)=f(b),
.由.f(a)=f(b),得
 ,即
,即 ,所以
,所以 ,
,解得ab=1.所以abc=c∈(2,
 ),所以abc的取值范围是(2,
),所以abc的取值范围是(2, ),选C.
),选C.故选C.
点评:本题考查函数对数函数的图象与性质,以及根据函数与方程的关系求参数的取值范围问题.利用数形结合思想是解决这类问题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目







 ,若a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是 .
,若a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是 . ,若a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是 .
,若a,b,c,d互不相等,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是 . ,若a、b、c均不相等且
,若a、b、c均不相等且 ,则abc的取值范围为 ( )
,则abc的取值范围为 ( ) ,若a、b、c的值互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
,若a、b、c的值互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )