题目内容
某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:
的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位: ),
), (单位:弧度).
(单位:弧度).

(I)将S表示为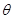 的函数;
的函数;
(II)当绿化面积S最大时,试确定点A的位置,并求最大面积.
 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:
的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位: ),
), (单位:弧度).
(单位:弧度).
(I)将S表示为
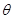 的函数;
的函数;(II)当绿化面积S最大时,试确定点A的位置,并求最大面积.
(Ⅰ)
 (Ⅱ)
(Ⅱ) .
.

 (Ⅱ)
(Ⅱ) .
.试题分析:(Ⅰ)根据三角函数的定义,确定直角三角形两直角边长
 ,
,即得到S表示为
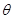 的函数.
的函数.(Ⅱ)通过“求导数,求驻点,研究区间导数值的正负,确定极值,最值”.“表解法”形象直观,易于理解.
试题解析:(Ⅰ)如图,
 ,
,
 . 3分
. 3分则

 6分
6分(Ⅱ)
 令
令 ,
,得cos
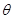 =
= 或cos
或cos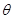 =-1(舍去),
=-1(舍去),此时
 . 8分
. 8分当
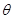 变化时,S′,S的变化情况如下表:
变化时,S′,S的变化情况如下表: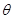 |  |  |  |
 | + | 0 | - |
 |  ? ? | 极大值 |  |
 时,S取得最大值
时,S取得最大值 ,此时
,此时 ,即点A到北京路一边
,即点A到北京路一边 的距离为
的距离为 . 13分
. 13分
练习册系列答案
相关题目
 .
. ,求
,求 在点
在点 处的切线方程;
处的切线方程; 恒成立,求
恒成立,求 的取值范围.
的取值范围. ,
, .
.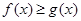 恒成立,求实数
恒成立,求实数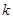 的值;
的值;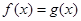 有一根为
有一根为 ,方程
,方程 的根为
的根为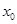 ,是否存在实数
,是否存在实数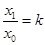 ?若存在,求出所有满足条件的
?若存在,求出所有满足条件的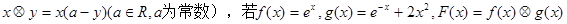
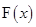 的解析式;
的解析式;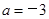 ,在
,在 的图像在点
的图像在点 处的切线方程为
处的切线方程为 .
. ,
, 的值;
的值; 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 排水管,在路南侧沿直线
排水管,在路南侧沿直线 排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将
排水管(假设水管与公路的南,北侧在一条直线上且水管的大小看作为一条直线),现要在矩形区域ABCD内沿直线EF将 m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为
m,公路两侧排管费用为每米1万元,穿过公路的EF部分的排管费用为每米2万元,设EF与AB所成角为 .矩形区域内的排管费用为W.
.矩形区域内的排管费用为W.
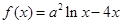 ,
,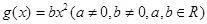 .
.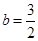 时,函数
时,函数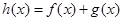 在
在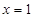 处有极小值,求函数
处有极小值,求函数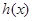 的单调递增区间;
的单调递增区间;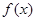 和
和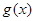 有相同的极大值,且函数
有相同的极大值,且函数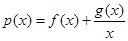 在区间
在区间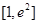 上的最大值为
上的最大值为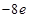 ,求实数
,求实数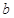 的值(其中
的值(其中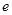 是自然对数的底数).
是自然对数的底数). ,
, 是函数
是函数 图象上不同于
图象上不同于 的一点.有如下结论:
的一点.有如下结论: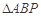 是等腰三角形;
是等腰三角形; 与函数
与函数 的图象分别交于点A、B,则|AB|的最小值为 ( )
的图象分别交于点A、B,则|AB|的最小值为 ( )  B.
B. C.
C.  D.
D.