题目内容
定义max{x1，x2}表示x1，x2中较大的那个数，则当x∈R时，函数f（x）=max{2-x2，x}（其中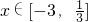
）的最大值与最小值的差是________．
9
分析：根据新定义，已知x∈[-3，
]，分别求出函数2-x2和x的最值，求出最大值与最小值．
解答：∵实数x1，x2，max{x1，x2}表示x1，x2中较大的那个数，
∵x∈[-3，]，
∴对于2-x2，当x=0时有最大值为2，当x=-3时有最小值为-7，
对于x，当x=时有最大值为，当x=-3时有最小值为-3，
∴f（x）=max{2-x2，x}=2，最小值为-7，
则最大值与最小值的差是9，
故答案为9．
点评：本题是一道新定义题，考查了函数的最值及其几何意义，是道基础题．
分析：根据新定义，已知x∈[-3，
]，分别求出函数2-x2和x的最值，求出最大值与最小值．解答：∵实数x1，x2，max{x1，x2}表示x1，x2中较大的那个数，
∵x∈[-3，
]，∴对于2-x2，当x=0时有最大值为2，当x=-3时有最小值为-7，
对于x，当x=
时有最大值为，当x=-3时有最小值为-3，∴f（x）=max{2-x2，x}=2，最小值为-7，
则最大值与最小值的差是9，
故答案为9．
点评：本题是一道新定义题，考查了函数的最值及其几何意义，是道基础题．
练习册系列答案
名题金卷系列答案
相关题目
记实数x1，x2，…xn中的最大数为max{x1，x2，…xn}，最小数为min{x1，x2，…xn}．已知△ABC的三边边长为a、b、c（a≤b≤c），定义它的倾斜度为t=max{
，
，
}•min{
，
，
}，x，则“t=1”是“△ABC为等边三角形”的（ ）
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| b |
| c |
| c |
| a |
| A、充分布不必要的条件 |
| B、必要而不充分的条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
）的最大值与最小值的差是 ．