Question

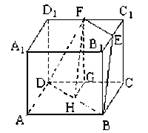
（14分）如图2－72，棱长为a的正方体ABCD－A₁B₁C₁D₁中，E、F分别是B₁C₁、C₁D₁的中点，

（1）求证：E、F、B、D四点共面；

（2）求四边形EFDB的面积．

 

Answer 1

【答案】

（1）见解析；（2）＝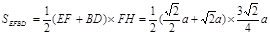

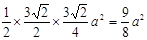
【解析】

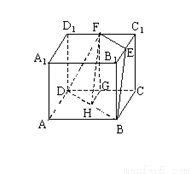
试题分析：⑴证明：如答图所示，连结B₁D₁，在△C₁B₁D₁中，C₁E＝EB₁，C₁F＝FD₁ ，∴EF//B₁D₁，且EF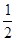＝B₁D₁，又A₁A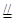B₁B，A₁A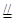D₁D，∴B₁B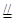D₁D，∴四边形BB₁D₁D是平行四边形. ∴B₁D//BD，EF//BD，∴E、F、D、B四点共面

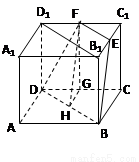
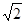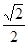⑵由AB＝a，知BD＝B₁D₁＝a，EF＝a，

DF＝BE＝＝，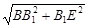

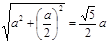过F作FH⊥DB于H，则DH＝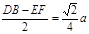

∴FH＝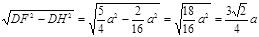

四边形的面积为＝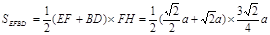

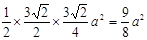
考点：本题主要考查正方体的特征、平面的基本性质以及平面图形的面积计算，考查空间想象能力及逻辑推理论证能力。

点评：空间问题注意转化成平面问题，这是解答立体几何问题的基本思路。