Question

双曲线过点P(2,-6)、Q(3,4).求双曲线的标准方程.

Answer 1

解法一:若焦点在x轴上时,设双曲线的标准方程为-=1(a＞0,b＞0),

∵双曲线过点P(2,-6)、Q(3,4),

∴

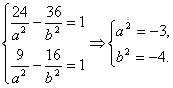
∵a²、b²都为正值,

∴焦点不在x轴上,故焦点在y轴上.

设双曲线的标准方程为=1(a＞0,b＞0).

又∵双曲线过点P(2,-6)、Q(3,4),代入,得a²=4,b²=3.

故所求的双曲线的标准方程为-=1.

解法二:设所求的双曲线的标准方程为mx²+ny²=1(m、n＜0),

∵双曲线过点P(2,-6)、Q(3,4),

则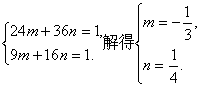

故所求双曲线的标准方程为-=1.