题目内容
已知a>0,n为正整数,
(Ⅰ)设y=(x-a)n,证明y′=n(x-a)n-1;
(Ⅱ)设fn(x)=xn-(x-a)n,对任意n≥a,证明fn+1′(n+1)>(n+1)fn′(n)。
(Ⅰ)设y=(x-a)n,证明y′=n(x-a)n-1;
(Ⅱ)设fn(x)=xn-(x-a)n,对任意n≥a,证明fn+1′(n+1)>(n+1)fn′(n)。
证明:(Ⅰ)因为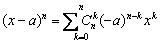 ,
,
所以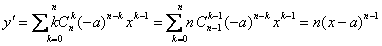 ;
;
(Ⅱ)对函数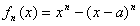 ,求导数:
,求导数: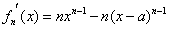 ,
,
所以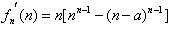 ,
,
当x≥a>0时,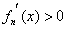 ,
,
∴当x≥a时,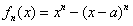 是关于x的增函数,
是关于x的增函数,
因此,当n≥a时,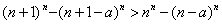 ,
,
∴
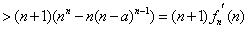 ,
,
即对任意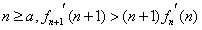 。
。
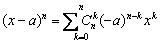 ,
,所以
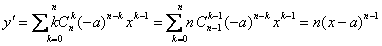 ;
;(Ⅱ)对函数
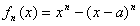 ,求导数:
,求导数: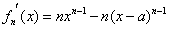 ,
,所以
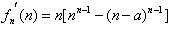 ,
,当x≥a>0时,
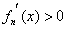 ,
,∴当x≥a时,
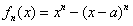 是关于x的增函数,
是关于x的增函数,因此,当n≥a时,
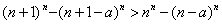 ,
,∴

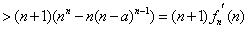 ,
,即对任意
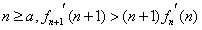 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目