Question

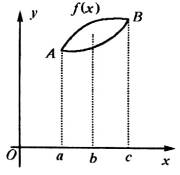
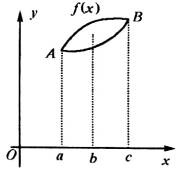
函数（），一段图像如下图所示：

（I）分别求出A、、的值并确定函数的解析式；

（1I）求的单调递减区间，并指出取最大值时的集合；

（Ⅲ）把的图像向左至少平移多少个单位，才能使得到的图像所对应的函数 为偶函数？

Answer 1

解：（I）由图像可知A=3，

∵，∴

∴            

∵图像过点（，0），则

∴

又，∴         

∴                

（Ⅱ）由（Ⅰ）知，

故

解得

所以的单调递减区间为

当时，取最大值3

此时，所以

则取最大值时，

的取值集合是

（Ⅲ）因为

 

                          

所以把函数的图像至少向左平移个单位，

使得到的图像所对应的函数为偶函数。