题目内容
【题目】已知命题:“![]() ,使等式
,使等式![]() 成立”是真命题.
成立”是真命题.
(1)求实数![]() 的取值集合
的取值集合![]() ;
;
(2)设不等式![]() 的解集为
的解集为![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
试题分析:(1)题中命题为真,说明方程![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解,因此只要求
上有解,因此只要求![]() 在
在![]() 上的值域即可;(2)由充分必要条件与集合的关系得
上的值域即可;(2)由充分必要条件与集合的关系得![]() 且
且![]() ,因此可通过分类解不等式得集合
,因此可通过分类解不等式得集合![]() ,再利用子集关系可求得
,再利用子集关系可求得![]() 的范围.
的范围.
试题解析:(1)由题意知,方程![]() 在
在![]() 上有解,即
上有解,即![]() 的取值范围就是函数
的取值范围就是函数![]() 在
在![]() 上的值域,易得
上的值域,易得![]() .
.
(2)因为![]() 是
是![]() 的必要不充分条件,所以
的必要不充分条件,所以![]() 且
且![]()
若![]() ,分以下几种情形研究;
,分以下几种情形研究;
①当![]() 时,解集
时,解集![]() 为空集,不满足题意,
为空集,不满足题意,
②当![]() 时,
时,![]() ,此时集合
,此时集合![]() ,
,
则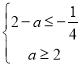 解得
解得![]() ,且
,且![]() 时,
时,![]() ,故
,故![]() 满足题意,
满足题意,
③当![]() 时,
时,![]() ,此时集合
,此时集合![]() ,
,
则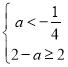 ,解得
,解得![]() .
.
综上,![]() 或
或![]() 时
时![]() 是
是![]() 的必要不充分条件.
的必要不充分条件.

练习册系列答案
相关题目
【题目】某地为弘扬中国传统文化举办“传统文化常识问答活动”,随机对该市![]() 岁的人群抽取一个容量为
岁的人群抽取一个容量为![]() 的样本,并将样本数据分成五组:
的样本,并将样本数据分成五组: ![]() ,再将其按从左到右的顺序分别编号为第
,再将其按从左到右的顺序分别编号为第![]() 组,第
组,第![]() 组,…,第
组,…,第![]() 组,绘制了样本的频率分布直方图,并对回答问题情况进行统计后,结果如下表所示.
组,绘制了样本的频率分布直方图,并对回答问题情况进行统计后,结果如下表所示.
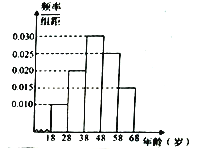
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的比例 |
第 | |
|
|
第 | |
|
|
第 | |
|
|
第 | |
|
|
第 | |
|
|
⑴分别求出![]() ,
, ![]() 的值;
的值;
⑵从![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,则第
人,则第![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
⑶在⑵的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求所抽取的人中第
人颁发幸运奖,求所抽取的人中第![]() 组至少有
组至少有![]() 人获得幸运奖的概率.
人获得幸运奖的概率.