Question

【题目】已知函数相邻两对称轴间的距离为，若将的图象先向左平移个单位，再向下平移1个单位，所得的函数为奇函数.

（1）求的解析式，并求的对称中心；

（2）若关于的方程在区间上有两个不相等的实根，求实数的取值范围.

Answer 1

【答案】（1）；对称中心为：，（2）或

【解析】

（1）由周期求得，由函数的图象变换规律可得，再根据的为奇函数求得和的值，可得和的解析式以及的对称中心．

（2）由（1）可得，由题意可得可得关于的方程在区间上有唯一解．再利用二次函数的性质求得的范围．

解：（1）由条件得：，

即，

则，

又为奇函数，

则，，

，，

令，，解得，，

故函数的对称中心为：，

（2），又有（1）知，则，

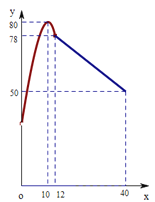
的函数值从递增到，又从递减回.

令，则

由原命题得：在上仅有一个实根.

令，

则需或，

解得：或.