题目内容
若| sin(π-α)cos(2π-α) | ||
tan(π-α)sin(
|
| ||
| 3 |
求(1)
| cosα-sinα |
| cosα+sinα |
(2)1-sinαcosα+cos2α的值.
分析:(1)直接利用诱导公式求出cosα,求出sinα,然后求出
;
(2)利用(1)的结论,代入1-sinαcosα+cos2α,求出值即可.
| cosα-sinα |
| cosα+sinα |
(2)利用(1)的结论,代入1-sinαcosα+cos2α,求出值即可.
解答:解:(1)将
=-
化简,得cosα=
∵α∈(0,π)∴可求得tanα=
,
∴
=
=
=
=2
-3;
(2)1-sinαcosα+cos2α=1+
=1+
=1+
=
.
| sin(π-α)cos(2π-α) | ||
tan(π-α)sin(
|
| ||
| 3 |
| ||
| 3 |
∵α∈(0,π)∴可求得tanα=
| 2 |
∴
| cosα-sinα |
| cosα+sinα |
1-
| ||
1+
|
| 1-tanα |
| 1+tanα |
1-
| ||
1+
|
| 2 |
(2)1-sinαcosα+cos2α=1+
| -sinαcosα+cos2α |
| sin2α+cos2α |
=1+
-
| ||
|
-
| ||
| 2+1 |
4-
| ||
| 3 |
点评:正确利用诱导公式化简表达式是解题的关键,注意三角函数的角的范围求出三角函数的值,考查计算能力.

练习册系列答案
相关题目
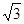 ,且c =
,且c =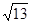 ,C =
,C =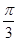 ,求a,b的值
,求a,b的值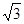 ,且c =
,且c =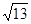 ,C =
,C =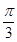 ,求a,b的值.
,求a,b的值.  .
. ,试判断△ABC的形状并说明理由
,试判断△ABC的形状并说明理由 .
. ,试判断△ABC的形状并说明理由
,试判断△ABC的形状并说明理由