题目内容
已知定义在R上的函数f(x)既是奇函数,又是周期为3的周期函数,当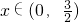 时,
时, ,则函数f(x)在区间[0,6]上的零点个数为________个.
,则函数f(x)在区间[0,6]上的零点个数为________个.
9
分析:要求方程f(x)=0在区间[0,6]上的解的个数,根据函数f(x)是定义域为R的周期为3的奇函数,且当x∈(0, )时f(x)=sinπx,我们不难得到一个周期函数零点的个数,根据周期性进行分析不难得到结论.
)时f(x)=sinπx,我们不难得到一个周期函数零点的个数,根据周期性进行分析不难得到结论.
解答:∵当x∈(0, )时,f(x)=sinπx,
)时,f(x)=sinπx,
令f(x)=0,则sinπx=0,解得x=1.
又∵函数f(x)是定义域为R的奇函数,
∴在区间∈[- ,
, ]上,
]上,
f(-1)=f(1)=f( )=f(-
)=f(- )=0,
)=0,
f(0)=0,
∵函数f(x)是周期为3的周期函数,
则方程f(x)=0在区间[0,6]上的解有0,1, ,2,3,4,
,2,3,4, ,5,6.
,5,6.
共9个.
故答案为:9.
点评:若奇函数经过原点,则必有f(0)=0,这个关系式大大简化了解题过程,要注意在解题中使用.如果本题所给区间为开区间,则答案为7个,若区间为半开半闭区间,则答案为8个,故要注意对端点的分析.
分析:要求方程f(x)=0在区间[0,6]上的解的个数,根据函数f(x)是定义域为R的周期为3的奇函数,且当x∈(0,
 )时f(x)=sinπx,我们不难得到一个周期函数零点的个数,根据周期性进行分析不难得到结论.
)时f(x)=sinπx,我们不难得到一个周期函数零点的个数,根据周期性进行分析不难得到结论.解答:∵当x∈(0,
 )时,f(x)=sinπx,
)时,f(x)=sinπx,令f(x)=0,则sinπx=0,解得x=1.
又∵函数f(x)是定义域为R的奇函数,
∴在区间∈[-
 ,
, ]上,
]上,f(-1)=f(1)=f(
 )=f(-
)=f(- )=0,
)=0,f(0)=0,
∵函数f(x)是周期为3的周期函数,
则方程f(x)=0在区间[0,6]上的解有0,1,
 ,2,3,4,
,2,3,4, ,5,6.
,5,6.共9个.
故答案为:9.
点评:若奇函数经过原点,则必有f(0)=0,这个关系式大大简化了解题过程,要注意在解题中使用.如果本题所给区间为开区间,则答案为7个,若区间为半开半闭区间,则答案为8个,故要注意对端点的分析.

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |