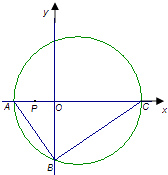
题目内容
【题目】已知直线l与椭圆 ![]() 交于两点A(x1 , y1),B(x2 , y2),椭圆上的点到下焦点距离的最大值、最小值分别为
交于两点A(x1 , y1),B(x2 , y2),椭圆上的点到下焦点距离的最大值、最小值分别为 ![]() ,向量
,向量 ![]() =(ax1 , by1),
=(ax1 , by1), ![]() =(ax2 , by2),且
=(ax2 , by2),且 ![]() ⊥
⊥ ![]() ,O为坐标原点. (Ⅰ)求椭圆的方程;
,O为坐标原点. (Ⅰ)求椭圆的方程;
(Ⅱ)判断△AOB的面积是否为定值,如果是,请给予证明;如果不是,请说明理由.
【答案】解:(Ⅰ)由题意可知 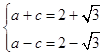 ,∴
,∴ 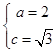 ,∴b2=a2﹣c2=1 ∴椭圆的方程为
,∴b2=a2﹣c2=1 ∴椭圆的方程为 ![]() ;
;
(Ⅱ)△AOB的面积为定值1.
∵ ![]() ,∴a2x1x2+b2y1y2=0,∴4x1x2+y1y2=0
,∴a2x1x2+b2y1y2=0,∴4x1x2+y1y2=0
① 若直线l斜率不存在,设直线l的方程为x=p,则x1=x2=p,y1=﹣y2 ,
∵4x1x2+y1y2=0,∴ ![]()
∵ ![]() ,∴
,∴ ![]()
∴S△AOB= ![]() =1;
=1;
②若直线l斜率存在,设直线l的方程为y=kx+r,代入椭圆方程,可得(4+k2)x2+2krx+r2﹣4=0
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]()
∵4x1x2+y1y2=0
∴(4+k2)x1x2+kr(x1+x2)+r2=0
∴r2﹣4﹣ ![]() +r2=0
+r2=0
∴2r2=4+k2 , ∴r2≥2
∴△=16(k2﹣r2+4)>0
设原点O到直线l的距离为d,则S△AOB= ![]() d|AB|=
d|AB|= ![]() ×
× ![]() =
= ![]()
综上可知,△AOB的面积为定值1.
【解析】(Ⅰ)利用椭圆上的点到下焦点距离的最大值、最小值分别为 ![]() ,确定椭圆的几何量,即可求得椭圆的方程;(Ⅱ)先利用向量知识,可得4x1x2+y1y2=0,再分类讨论,求出面积,即可求得结论.
,确定椭圆的几何量,即可求得椭圆的方程;(Ⅱ)先利用向量知识,可得4x1x2+y1y2=0,再分类讨论,求出面积,即可求得结论.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目