题目内容
已知 ,
, ,
, 分别为
分别为 三个内角
三个内角 ,
, ,
, 的对边,
的对边,  =
=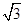
 sin
sin
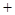
 cos
cos .
.
(1)求角 ;
;
(2)若 =
=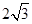 ,
, 的面积为
的面积为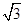 ,求
,求 的周长.
的周长.
(1) 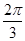 ;(2)
;(2) 
解析试题分析:(1) 根据正弦定理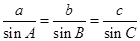 可将
可将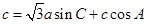 变形为
变形为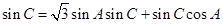 。因为角
。因为角 三角形的内角,所以
三角形的内角,所以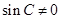 ,可将上式变形为
,可将上式变形为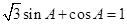 。用化一公式即两角和差公式的逆用将上式左边化简可得
。用化一公式即两角和差公式的逆用将上式左边化简可得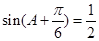 ,根据整体角
,根据整体角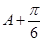 的范围可得
的范围可得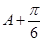 的值,即可得角
的值,即可得角 的值。 (2)由三角形面积
的值。 (2)由三角形面积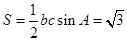 可得
可得 。再结合余弦定理可得
。再结合余弦定理可得 的值,解方程组可得
的值,解方程组可得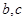 的值,从而可得三角形的周长。
的值,从而可得三角形的周长。
解(1)由 =
=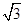
 sin
sin
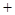
 cos
cos 及正弦定理得
及正弦定理得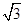 sin
sin sin
sin +cos
+cos sin
sin -sin
-sin =0,
=0,
由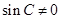 ,所以
,所以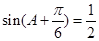 , 4分
, 4分
又0< <π,
<π,
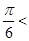
 +
+
 5分
5分
故 =
=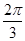 . 6分
. 6分
(2)△ABC的面积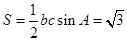 ,故
,故 . 8
. 8
由余弦定理知 2=
2= 2+
2+ 2-2
2-2
 cos
cos ,得
,得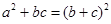
代入 =
=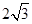 ,
,
 =4解得
=4解得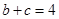 ,故三角形周长为
,故三角形周长为 .(解出
.(解出 ,
, 的值亦可)――12
的值亦可)――12
考点:1正弦定理;2三角形面积公式;3余弦定理。

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 中,
中, ,
,
 的值;
的值; 的长
的长
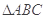 中,角
中,角 、
、 、
、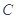 的对边分别为
的对边分别为 、
、 、
、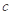 ,
, ,
, .
.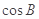 的值;(2) 设函数
的值;(2) 设函数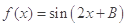 ,求
,求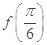 的值.
的值. b2.
b2. ,b=1时,求a,c的值;
,b=1时,求a,c的值;
 ,向量
,向量
 .
. ,b+c=3,求b,c的长.
,b+c=3,求b,c的长. 的内角
的内角 的对边分别为
的对边分别为 ,
, ,
, 大小(2)若
大小(2)若 ,求
,求 边上的高
边上的高
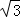 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.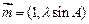 ,
,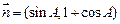 .已知
.已知 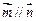 .
.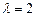 ,求角A的大小;
,求角A的大小;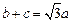 ,求
,求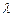 的取值范围。
的取值范围。