题目内容
已知点P（x，y）满足
，点Q（x，y）在圆（x+2）2+（y+2）2=1上，则|PQ|的最大值与最小值为（ ）
|
| A．6，3 | B．6，2 | C．5，3 | D．5，2 |
先根据约束条件画出可行域，
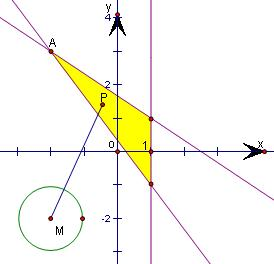
问题转化为区域内的点到圆心M（-2，-2）的最小值．
∵可行域内点P到圆心M（-2，-2）距离，
当点M到直线4x+3y-1=0的距离时，
z最小，最小值为
=3，
∴z=|PQ|的最小值=3-1=2，
由
得A（-2，3）
当点M到可行域内的点A（-2，3）距离时，
|MA|最大，最大值为|MA|=5，
∴z=|PQ|的最大值=5+1=6，
故选B．
问题转化为区域内的点到圆心M（-2，-2）的最小值．
∵可行域内点P到圆心M（-2，-2）距离，
当点M到直线4x+3y-1=0的距离时，
z最小，最小值为
| |4×(-2)+3×(-2)-1| | ||
|
∴z=|PQ|的最小值=3-1=2，
由
|
当点M到可行域内的点A（-2，3）距离时，
|MA|最大，最大值为|MA|=5，
∴z=|PQ|的最大值=5+1=6，
故选B．
练习册系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
已知点P（x，y）满足
，点Q在曲线y=
(x＜0)上运动，则|PQ|的最小值是（ ）
|
| 1 |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|