题目内容
7. 已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.
已知椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1.(I)以原点O为极点,x轴正半轴为极轴建立极坐标系,求椭圆C与直线l的极坐标方程;
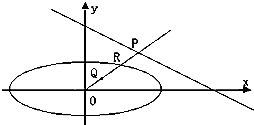
(Ⅱ)已知P是l上一动点,射线OP交椭圆C于点R,又点Q在OP上且满足|OQ|•|OP|=|OR|2.当点P在l上移动时,求点Q在直角坐标系下的轨迹方程.
分析 (I)将x=ρcosθ,y=ρsinθ分别代入椭圆方程和直线方程,化简整理即可得到极坐标方程;
(II)设Q(ρ,θ),由|OQ|•|OP|=|OR|2结合(Ⅰ)即可得到所求直角坐标方程.
解答 解:(I)椭圆C:$\frac{{x}^{2}}{24}$+$\frac{{y}^{2}}{16}$=1,直线l:$\frac{x}{12}$+$\frac{y}{8}$=1,
将x=ρcosθ,y=ρsinθ分别代入上式,化简可得,
C:${ρ^2}=\frac{48}{{2{{cos}^2}θ+3{{sin}^2}θ}}$,l:$ρ=\frac{24}{2cosθ+3sinθ}$;
(II)设Q(ρ,θ),
由|OQ|•|OP|=|OR|2
结合(Ⅰ)可得,ρ•$\frac{24}{2cosθ+3sinθ}$=$\frac{48}{2co{s}^{2}θ+3si{n}^{2}θ}$,
由x=ρcosθ,y=ρsinθ,可得
2x2+3y2-4x-6y=0.
点评 本题考查极坐标和直角坐标的互化,考查运算求解的能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
17.已知等差数列1,-1,-3,-5,…,则-89是它的第( )项.
| A. | 92 | B. | 47 | C. | 46 | D. | 45 |