题目内容
已知函数y=Asin(ωx+?)(A>0,ω>0,|?|<
)图象上的一个最高点为P(2,
),由这个最高点到相邻最低点间的曲线与x轴相交于点Q(6,0).
(1)求这个函数的表达式;
(2)求这个函数的单调区间.
| π |
| 2 |
| 2 |
(1)求这个函数的表达式;
(2)求这个函数的单调区间.
分析:(1)首先由曲线y=Asin(ωx+φ)的最高点求A,再由最高点与相邻的平衡点求最小正周期T,进一步求得ω,最后通过特殊点求φ,则问题解决.
(2)通过(1)的函数解析式,借助正弦函数的单调区间,求出函数的单调区间即可.
(2)通过(1)的函数解析式,借助正弦函数的单调区间,求出函数的单调区间即可.
解答:解:(1)由曲线y=Asin(ωx+φ)的一个最高点是(2,
),得A=
,
又最高点(2,
)到相邻的最低点间,曲线与x轴交于点(6,0),
则
=6-2=4,即T=16,所以ω=
=
.
此时y=
sin(
x+φ),
将x=2,y=
代入得
=
sin(
×2+φ),|?|<
,
+φ=
,
∴φ=
,
所以这条曲线的解析式为y=
sin(
x+
).
(2)因为
x+
∈[2kπ-
,2kπ+
],解得x∈[16k-6,2+16k],k∈Z.
所以函数的单调增区间为[-6+16k,2+16k],k∈Z,
因为
x+
∈[2kπ+
,2kπ+
],解得x∈[2+16k,10+16k],k∈Z,
所以函数的单调减区间为:[2+16k,10+16k],k∈Z,
| 2 |
| 2 |
又最高点(2,
| 2 |
则
| T |
| 4 |
| 2π |
| T |
| π |
| 8 |
此时y=
| 2 |
| π |
| 8 |
将x=2,y=
| 2 |
| 2 |
| 2 |
| π |
| 8 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴φ=
| π |
| 4 |
所以这条曲线的解析式为y=
| 2 |
| π |
| 8 |
| π |
| 4 |
(2)因为
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
所以函数的单调增区间为[-6+16k,2+16k],k∈Z,
因为
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
所以函数的单调减区间为:[2+16k,10+16k],k∈Z,
点评:本题主要考查由曲线y=Asin(ωx+φ)的部分信息求函数y=Asin(ωx+φ)的解析式的方法.函数单调区间的求法,考查计算能力.

练习册系列答案
相关题目
已知函数y=Asin(ωx+φ),在同一周期内,当x=
时,取最大值y=2,当x=
时,取得最小值y=-2,那么函数的解析式为( )
| π |
| 12 |
| 7π |
| 12 |
A、y=
| ||||
B、y=2sin(2x+
| ||||
C、y=2sin(
| ||||
D、y=2sin(2x+
|
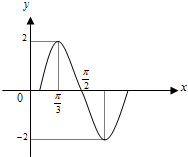 已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )
已知函数y=Asin(ωx+∅)(A>0,ω>0,-π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A、y=2sin(
| ||||
B、y=2sin(3x+
| ||||
C、y=2sin(3x-
| ||||
D、y=2sin(3x-
|
 已知函数
已知函数 已知函数
已知函数