题目内容

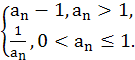若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T,已知数列{an}满足a1=m(m>0),an+1=则下列结论正确的有　　　　.

①若m=,则a5=3;②若a3=2,则m可以取3个不同的值;③若m=,则数列{an}是周期为3的数列;④∃m∈Q且m≥2,数列{an}是周期数列.

对于①,由a1=可得a2=,a3=,a4=4,a5=3,故①正确;对于②,当a3=2时,a2=3或a2=,若a2=3,则a1=4或a1=,若a2=,则a1=,故②正确;对于③,当a1=时,a2=-1,a3==+1,a4=,a5=-1,…,故③正确;对于④,若a1=m=2,则a2=1,a3=1,a4=1,…,故④错误.

答案:①②③

练习册系列答案
相关题目
若数列{an}满足a1=1，an+1=2an+n，则通项an=
3×2n-1-n-1
3×2n-1-n-1
．
设m＞3，对于数列{an} （n=1，2，…，m，…），令bk为a1，a2，…，ak中的最大值，称数列 {bn} 为{an} 的“递进上限数列”．例如数列2，1，3，7，5的递进上限数列为2，2，3，7，7．则下面命题中
①若数列{an} 满足an+3=an，则数列{an} 的递进上限数列必是常数列；
②等差数列{an} 的递进上限数列一定仍是等差数列
③等比数列{an} 的递进上限数列一定仍是等比数列
正确命题的个数是（　　）
（2009•烟台二模）若数列{an}满足an+12-
a
2
n
=d（d为正常数，n∈N+），则称{an}为“等方差数列”．甲：数列{an}为等方差数列；乙：数列{an}为等差数列，则甲是乙的（　　）
（2009•潍坊二模）已知函数f（x）=ax-
ln(1+x)
1+x
在x=0处取得极值．
（I）求实数a的值，并判断，f（x）在[0，+∞）上的单调性；
（Ⅱ）若数列{an}满足a1=1，an+1=f（an），求证：0＜an+1＜an≤l；
（Ⅲ）在（II）的条件．下，记sn=
a1
1+a1
+
a1．a2
(1+a1)(1+a2)
+…+
a1．a2…an
(1+a1)(1+a2)…(1+an)
，求证：sn＜1．
已知函数f（x）=
x
x+1
，若数列{an}满足：an＞0，a1=1，an+1=[f（
an
）]2，
（I）求数列{an}的通项公式数列an；
（II）若数列{an}的前n项和为Sn，证明：Sn＜2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网