题目内容
已知函数f(x)=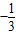 ax3+x2+2(a≠0).
ax3+x2+2(a≠0).(Ⅰ) 试讨论函数f(x)的单调性;
(Ⅱ) 若a>0,求函数f(x)在[1,2]上的最大值..
【答案】分析:(Ⅰ)已知f(x)的解析式,利用导数研究其单调性,对a进行讨论,从而进行求解;
(Ⅱ)已知a>0,要求函数f(x)在[1,2]上的最大值,对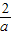 与1的大小进行讨论,根据(Ⅰ)的单调区间进行求解;
与1的大小进行讨论,根据(Ⅰ)的单调区间进行求解;
解答:解:(Ⅰ)∵f(x)=- ax3+x2+2(a≠0),
ax3+x2+2(a≠0),
∴f′(x)=-ax2+2x.
①当a>0时,令f′(x)>0,即-ax2+2x>0,得0<x<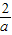 .
.
∴f(x)在(-∞,0),(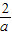 ,+∞)上是减函数,在(0,
,+∞)上是减函数,在(0,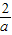 )上是增函数.
)上是增函数.
②当a<0时,令f′(x)>0,即-ax2+2x>0,得x>0,或x<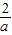 .
.
∴f(x)在(-∞,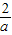 ),(0,+∞)上是增函数,在(
),(0,+∞)上是增函数,在(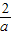 ,0)上是减函数.
,0)上是减函数.
(2)由(Ⅱ)得:
①当0<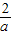 <1,即a>2时,f(x)在(1,2)上是减函数,
<1,即a>2时,f(x)在(1,2)上是减函数,
∴f(x)max=f(1)=3-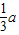
②当1≤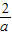 ≤2,即1≤a≤2时,f(x)在(1,
≤2,即1≤a≤2时,f(x)在(1,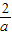 )上是增函数,在(
)上是增函数,在(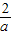 ,2)上是减函数,
,2)上是减函数,
∴f(x)max=f(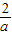 )=
)=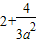 .
.
③当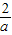 >2时,即0<a<1时,f(x)在(1,2)上是增函数,
>2时,即0<a<1时,f(x)在(1,2)上是增函数,
∴f(x)max=f(2)=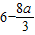 .
.
综上所述,当0<a<1时,f(x)的最大值为3-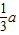 ,
,
当1≤a≤2时,f(x)的最大值为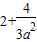 ,
,
当a>2时,f(x)的最大值为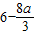 .
.
点评:本题考查了利用导数求闭区间上函数的最值,求函数在区间(a,b)上的最大值与最小值是通过比较函数在(a,b)内所有极值,此题还利用了分类讨论的思想,难度中等;
(Ⅱ)已知a>0,要求函数f(x)在[1,2]上的最大值,对
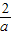 与1的大小进行讨论,根据(Ⅰ)的单调区间进行求解;
与1的大小进行讨论,根据(Ⅰ)的单调区间进行求解;解答:解:(Ⅰ)∵f(x)=-
 ax3+x2+2(a≠0),
ax3+x2+2(a≠0),∴f′(x)=-ax2+2x.
①当a>0时,令f′(x)>0,即-ax2+2x>0,得0<x<
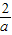 .
.∴f(x)在(-∞,0),(
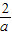 ,+∞)上是减函数,在(0,
,+∞)上是减函数,在(0,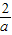 )上是增函数.
)上是增函数.②当a<0时,令f′(x)>0,即-ax2+2x>0,得x>0,或x<
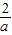 .
.∴f(x)在(-∞,
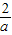 ),(0,+∞)上是增函数,在(
),(0,+∞)上是增函数,在(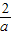 ,0)上是减函数.
,0)上是减函数.(2)由(Ⅱ)得:
①当0<
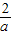 <1,即a>2时,f(x)在(1,2)上是减函数,
<1,即a>2时,f(x)在(1,2)上是减函数,∴f(x)max=f(1)=3-
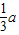
②当1≤
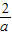 ≤2,即1≤a≤2时,f(x)在(1,
≤2,即1≤a≤2时,f(x)在(1,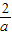 )上是增函数,在(
)上是增函数,在(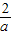 ,2)上是减函数,
,2)上是减函数,∴f(x)max=f(
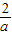 )=
)=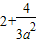 .
.③当
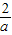 >2时,即0<a<1时,f(x)在(1,2)上是增函数,
>2时,即0<a<1时,f(x)在(1,2)上是增函数,∴f(x)max=f(2)=
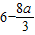 .
.综上所述,当0<a<1时,f(x)的最大值为3-
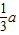 ,
,当1≤a≤2时,f(x)的最大值为
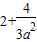 ,
,当a>2时,f(x)的最大值为
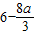 .
.点评:本题考查了利用导数求闭区间上函数的最值,求函数在区间(a,b)上的最大值与最小值是通过比较函数在(a,b)内所有极值,此题还利用了分类讨论的思想,难度中等;

练习册系列答案
相关题目