题目内容
e,π分别是自然对数的底和圆周率,则下列不等式不成立的是( )
分析:对A使用基本不等式,即可判断出正确.
对B使用基本不等式,即可判断出正确.
对D使用基本不等式,即可判断出正确.或通过作差法即可判断出.
故不成立的应是答案C.或直接判断其错误亦可.
对B使用基本不等式,即可判断出正确.
对D使用基本不等式,即可判断出正确.或通过作差法即可判断出.
故不成立的应是答案C.或直接判断其错误亦可.
解答:解:A.∵logπe=
>0,∴(logπe)2+
>2.故A正确;
B.∵logπe>0,logeπ>0,∴logπ
+loge
=
(logπe+logeπ)≥
=1,故B正确;
C.∵y=ex-x,y′=ex-1,x>1时y′>0,函数是增函数,∵e<π,∴ee<eπ,∴ee-e<eπ-π,故C不成立.
D.∵e2+π2>2eπ,∴2(e2+π2)>e2+2eπ+π2=(e+π)2,∴D正确.
故选C.
| 1 |
| logeπ |
| 1 |
| (logπe)2 |
B.∵logπe>0,logeπ>0,∴logπ
| e |
| π |
| 1 |
| 2 |
| logπe•logeπ |
C.∵y=ex-x,y′=ex-1,x>1时y′>0,函数是增函数,∵e<π,∴ee<eπ,∴ee-e<eπ-π,故C不成立.
D.∵e2+π2>2eπ,∴2(e2+π2)>e2+2eπ+π2=(e+π)2,∴D正确.
故选C.
点评:本题考查函数的基本性质,掌握重要不等式和基本不等式是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
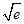 >
>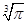 B.
B.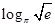 +
+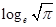 >1
>1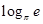 )
)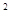 +
+ >2 D.
>2 D.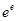 -e>
-e>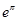 -π
-π