题目内容
已知U=R，A={x||x-3|＜2}，B={x|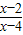
＞0}，求A∩B，CU（A∪B）．
【答案】分析：根据绝对值的性质和不等式的解法分别解出集合A，B，再根据交集和并集、补集的定义进行求解；
解答：解：∵U=R，A={x||x-3|＜2}，B={x|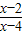
＞0}，
∴A={x||x-3|＜2}={x|1＜x＜5}，
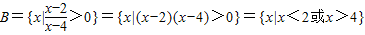
∴A∩B={x|1＜x＜2或4＜x＜5}，
∵A∪B=R，
∴CU（A∪B）=∅；
点评：此题主要考查不等式的解法，以及集合交、并、补的运算法则，是一道基础题；
解答：解：∵U=R，A={x||x-3|＜2}，B={x|
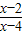＞0}，∴A={x||x-3|＜2}={x|1＜x＜5}，
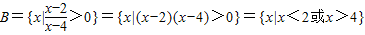
∴A∩B={x|1＜x＜2或4＜x＜5}，
∵A∪B=R，
∴CU（A∪B）=∅；
点评：此题主要考查不等式的解法，以及集合交、并、补的运算法则，是一道基础题；
练习册系列答案
寒假天地重庆出版社系列答案
相关题目