题目内容

（2010•成都一模）若x∈（0，+∞），则函数y=x+
2
x
的最小值为
2
2
2
2
．
分析：本题满足均值不等式的条件，用均值不等式即可求最值
解答：解：∵x∈（0，+∞）
∴y=x+
2
x
≥2
x•
2
x
=2
2

当x=
2
x
，即x=
2
时等号成立
故答案为：2
2
点评：本题考查均值不等式，用均值不等式时须满足“一正、二定、三相等”．属简单题
练习册系列答案
相关题目
（2010•成都一模）把正整数排列成如图甲三角形数阵，然后擦去第偶数行中的奇数和第奇数行中的偶数，得到如图乙的三角形数阵，再把图乙中的数按从小到大的顺序排成一列，得到一个数列{an}，若an=2009，则n=（　　）
（2010•成都一模）在等差数列{an}中，a1+a2=3，a2+a5=5，则公差为d的值为（　　）
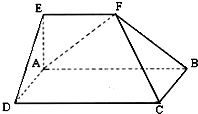（2010•成都一模）如图，在多面体ABCDEF中，四边形ABCD是矩形，在四边形ABFE中，AB∥EF，∠EAB=90°，AB=4，AD=AE=EF=2，平面ABFE⊥平面ABCD．
（1）求证：AF⊥平面BCF；
（2）求二面角B-FC-D的大小．
（2010•成都一模）已知函数f(x)=
1
3
x3-mx2-3m2x+1在区间（1，2）内是增函数，则实数m的取值范围是（　　）
（2010•成都一模）已知a∈(0，π)，cos(π+a)=
3
5
，则sina=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网