题目内容
方程x+
=
a在x∈(0,+∞)内有解,则实数a的取值范围是( )
| 2 |
| x |
| 2 |
分析:方程x+
=
a在x∈(0,+∞)内有解?
a≥(x+
)min,(x>0),利用基本不等式求出其最小值即可.
| 2 |
| x |
| 2 |
| 2 |
| 2 |
| x |
解答:解:∵方程x+
=
a在x∈(0,+∞)内有解?
a≥(x+
)min,(x>0)
∵x>0,∴x+
≥2
,当且仅当x=
是取等号.
∴
a≥2
.
∴a≥2.
故选B.
| 2 |
| x |
| 2 |
| 2 |
| 2 |
| x |
∵x>0,∴x+
| 2 |
| x |
x•
|
| 2 |
∴
| 2 |
| 2 |
∴a≥2.
故选B.
点评:把问题正确等价转化及熟练掌握基本不等式是解题的关键.

练习册系列答案
相关题目
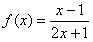 的对称中心是
的对称中心是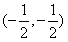 ;
;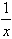 +k=0在x∈(0,1)没有实数根,则k的取值范围是k≥2;
+k=0在x∈(0,1)没有实数根,则k的取值范围是k≥2;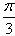 )的图像向右平移ψ(ψ>0)个单位后变为偶函数,则ψ的最小值是
)的图像向右平移ψ(ψ>0)个单位后变为偶函数,则ψ的最小值是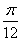 ,其中正确的结论是:( )。
,其中正确的结论是:( )。