题目内容
如图程序输出的n的值是分析：根据伪代码运行程序得j=1≤8，执行循环j=2，判定2 MOD 4是否为0，是0则统计1个，不是就不统计，j=3，依此类推，当不满足j≤8时，输出n的值即可．
解答：解：j=1≤8，执行循环j=2，2 MOD 4≠0，j=3，
j=3≤8，执行循环j=4，4 MOD 4=0，n=1，j=5，
j=5≤8，执行循环j=6，6 MOD 4≠0，j=7，
j=7≤8，执行循环j=8，8 MOD 4=0，n=2，j=9，
j=9＞8退出循环，
输出n=2．
故答案为：2．
j=3≤8，执行循环j=4，4 MOD 4=0，n=1，j=5，
j=5≤8，执行循环j=6，6 MOD 4≠0，j=7，
j=7≤8，执行循环j=8，8 MOD 4=0，n=2，j=9，
j=9＞8退出循环，
输出n=2．
故答案为：2．
点评：本题主要考查了当型循环，以及条件语句和程序框图，解题的关键弄清循环的次数，属于中档题．
练习册系列答案
相关题目
根据如图所示的程序框图，输入一个正整数n，将输出的x值依次记为x1，x2，x3，…，xn；输出的y值依次记为y1，y2，y3，…，yn．
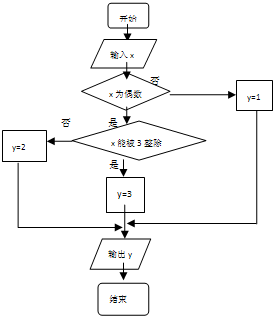
（2013•四川）某算法的程序框图如图所示，其中输入的变量x在1，2，3，…，24这24个整数中等可能随机产生．（12分）某算法的程序框图如图所示，其中输入的变量x在1，2，3，…，24这24个整数中等可能随机产生．
（Ⅰ）分别求出按程序框图正确编程运行时输出y的值为i的概率Pi（i=1，2，3）；
（Ⅱ）甲、乙两同学依据自己对程序框图的理解，各自编写程序重复运行n次后，统计记录了输出y的值为i（i=1，2，3）的频数．以下是甲、乙所作频数统计表的部分数据．
甲的频数统计表（部分）
|
运行 次数n |
输出y的值 为1的频数 |
输出y的值 为2的频数 |
输出y的值 为3的频数 |
|
30 |
14 |
6 |
10 |
|
… |
… |
… |
… |
|
2100 |
1027 |
376 |
697 |
乙的频数统计表（部分）
|
运行 次数n |
输出y的值 为1的频数 |
输出y的值 为2的频数 |
输出y的值 为3的频数 |
|
30 |
12 |
11 |
7 |
|
… |
… |
… |
… |
|
2100 |
1051 |
696 |
353 |
当n=2100时，根据表中的数据，分别写出甲、乙所编程序各自输出y的值为i（i=1，2，3）的频率（用分数表示），并判断两位同学中哪一位所编写程序符合算法要求的可能性较大．
