题目内容
椭圆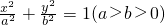 的中心、右焦点、右顶点及在准线与x轴的交点依次为O、F、G、H,则
的中心、右焦点、右顶点及在准线与x轴的交点依次为O、F、G、H,则 的最大值为
的最大值为
- A.

- B.

- C.

- D.不确定
C
分析:根据椭圆的标准方程,结合焦点坐标和准线方程的公式,可得|FG|=a-c,|OH|= ,所以
,所以 =
= =
= ,最后根据二次函数的性质结合
,最后根据二次函数的性质结合 ,可求出
,可求出 的最大值.
的最大值.
解答:∵椭圆方程为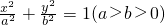
∴椭圆的右焦点是F(c,0),右顶点是G(a,0),右准线方程为x= ,其中c2=a2-b2.
,其中c2=a2-b2.
由此可得H( ,0),|FG|=a-c,|OH|=
,0),|FG|=a-c,|OH|=
∴ =
= =
= =
= =-(
=-( )2+
)2+
∵
∴当且仅当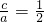 时,
时, 的最大值为
的最大值为
故选C
点评:本题根据椭圆的焦点坐标和准线方程,求线段比值的最大值,着重考查了椭圆的基本概念的简单性质,属于基础题.
分析:根据椭圆的标准方程,结合焦点坐标和准线方程的公式,可得|FG|=a-c,|OH|=
 ,所以
,所以 =
= =
= ,最后根据二次函数的性质结合
,最后根据二次函数的性质结合 ,可求出
,可求出 的最大值.
的最大值.解答:∵椭圆方程为
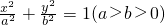
∴椭圆的右焦点是F(c,0),右顶点是G(a,0),右准线方程为x=
 ,其中c2=a2-b2.
,其中c2=a2-b2.由此可得H(
 ,0),|FG|=a-c,|OH|=
,0),|FG|=a-c,|OH|=
∴
 =
= =
= =
= =-(
=-( )2+
)2+
∵

∴当且仅当
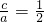 时,
时, 的最大值为
的最大值为
故选C
点评:本题根据椭圆的焦点坐标和准线方程,求线段比值的最大值,着重考查了椭圆的基本概念的简单性质,属于基础题.

练习册系列答案
相关题目
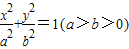 的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则
的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则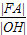 的最大值为( )
的最大值为( )


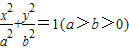 的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则
的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则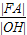 的最大值为( )
的最大值为( )


 的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则
的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则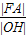 的最大值为( )
的最大值为( )


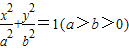 的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则
的中心、右焦点、右顶点、右准线与x轴的交点依次为O、F、A、H,则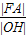 的最大值为( )
的最大值为( )

