题目内容
已知函数f(x)=sin(ωx+ϕ)(ω>0,0≤ϕ≤π)为偶函数,且其图象上相邻两对称轴之间的距离为π.(I)求函数f(x)的表达式.
(II)若
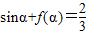 ,求
,求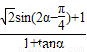 的值.
的值.
【答案】分析:(I)函数是偶函数,求出ϕ,利用图象上相邻两对称轴之间的距离为π,求出ω,即可求得函数f(x)的表达式.
(II)利用两角和的正弦以及弦切互化,化简 为sinαcosα,应用
为sinαcosα,应用 ,求出所求结果即可.
,求出所求结果即可.
解答:解:(I)∵f(x)为偶函数
∴sin(-ωx+ϕ)=sin(ωx+ϕ)
即2sinωxcosϕ=0恒成立
∴cosϕ=0,
又∵ (3分)
(3分)
又其图象上相邻对称轴之间的距离为π
∴T=2π∴ω=1
∴f(x)=cosx(6分)
(II)∵原式= (10分)
(10分)
又∵ (11分)
(11分)
即 ,故原式=
,故原式= (12分)
(12分)
点评:本题考查三角函数的周期性及其求法,同角三角函数基本关系的运用,考查计算能力,是基础题.
(II)利用两角和的正弦以及弦切互化,化简
 为sinαcosα,应用
为sinαcosα,应用 ,求出所求结果即可.
,求出所求结果即可.解答:解:(I)∵f(x)为偶函数
∴sin(-ωx+ϕ)=sin(ωx+ϕ)
即2sinωxcosϕ=0恒成立
∴cosϕ=0,
又∵
 (3分)
(3分)又其图象上相邻对称轴之间的距离为π
∴T=2π∴ω=1
∴f(x)=cosx(6分)
(II)∵原式=
 (10分)
(10分)又∵
 (11分)
(11分)即
 ,故原式=
,故原式= (12分)
(12分)点评:本题考查三角函数的周期性及其求法,同角三角函数基本关系的运用,考查计算能力,是基础题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
