题目内容
已知a、b、m、n、x、y均为正数,且a≠b,若a、m、b、x成等差数列,a、n、b、y成等比数列,则有
- A.m>n,x>y
- B.m>n,x<y
- C.m<n,x<y
- D.m<n,x>y
B
分析:根据等差数列、等比数列的定义和性质,可得m= ,n=
,n= ,b=
,b=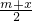 =
= ,由基本不等式求得 m>n,
,由基本不等式求得 m>n,
再根据 ≥
≥ 得到 y>x.
得到 y>x.
解答:a、b、m、n、x、y均为正数,且a≠b,且 a、m、b、x成等差数列,∴m= .
.
又 a、n、b、y成等比数列,∴n= ,由基本不等式可得 m>n.
,由基本不等式可得 m>n.
又 同理可得 b=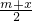 =
= ≥
≥ ,∴y>x.
,∴y>x.
综上,m>n,x<y,
故选B.
点评:本题考查等差数列的定义和性质,等比数列的定义和性质,基本不等式的应用,得到m= ,n=
,n= ,
,
b=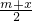 =
= ≥
≥ ,是解题的关键.
,是解题的关键.
分析:根据等差数列、等比数列的定义和性质,可得m=
 ,n=
,n= ,b=
,b=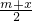 =
= ,由基本不等式求得 m>n,
,由基本不等式求得 m>n,再根据
 ≥
≥ 得到 y>x.
得到 y>x.解答:a、b、m、n、x、y均为正数,且a≠b,且 a、m、b、x成等差数列,∴m=
 .
.又 a、n、b、y成等比数列,∴n=
 ,由基本不等式可得 m>n.
,由基本不等式可得 m>n.又 同理可得 b=
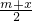 =
= ≥
≥ ,∴y>x.
,∴y>x.综上,m>n,x<y,
故选B.
点评:本题考查等差数列的定义和性质,等比数列的定义和性质,基本不等式的应用,得到m=
 ,n=
,n= ,
,b=
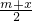 =
= ≥
≥ ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目
已知a、b、m、n、x、y均为正数,且a≠b,若a、m、b、x成等差数列,a、n、b、y成等比数列,则有( )
| A、m>n,x>y | B、m>n,x<y | C、m<n,x<y | D、m<n,x>y |