题目内容
已知函数f（x）是定义在R上的奇函数，当x＞0时，f（x）=log2x
（1）求f（x）的解析式；
（2）解关于x的不等式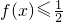
．
解：（1）设x＜0，则-x＞0
∵当x＞0时，f（x）=log2x
∴f（-x）=log2（-x），
又∵函数f（x）是奇函数
∴f（x）=-f（-x）=-log2（-x）．
当x=0时，f（0）=0
综上所述f（x）=
（2）由（1）得不等式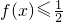可化为
x＞0时，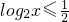
，解得0＜x≤
x=0时，0≤
，满足条件
x＜0时，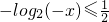
，解得x≤
综上所述原不等式的解集为{x|x≤，或0≤x≤}
分析：（1）设x＜0，则-x＞0，再由当x＞0时，f（x）=log2x-1求得f（-x）然后利用函数f（x）是奇函数得到f（x）．
（2）根据（1）中函数的解析式，分段解出各段上满足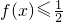的x的范围，综合分类讨论结果可得答案
点评：本题主要考查用奇偶性来求对称区间上的解析式，一定要注意，求哪一个区间的解析式，要在哪个区间上取变量．
∵当x＞0时，f（x）=log2x
∴f（-x）=log2（-x），
又∵函数f（x）是奇函数
∴f（x）=-f（-x）=-log2（-x）．
当x=0时，f（0）=0
综上所述f（x）=
（2）由（1）得不等式
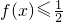可化为x＞0时，
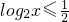，解得0＜x≤x=0时，0≤
，满足条件x＜0时，
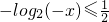，解得x≤综上所述原不等式的解集为{x|x≤
，或0≤x≤}分析：（1）设x＜0，则-x＞0，再由当x＞0时，f（x）=log2x-1求得f（-x）然后利用函数f（x）是奇函数得到f（x）．
（2）根据（1）中函数的解析式，分段解出各段上满足
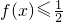的x的范围，综合分类讨论结果可得答案点评：本题主要考查用奇偶性来求对称区间上的解析式，一定要注意，求哪一个区间的解析式，要在哪个区间上取变量．
练习册系列答案
相关题目
已知函数f（x）=x+