Question

半径为

3

的球内有一个内接正三棱锥P-ABC，过球心O及一侧棱PA作截面截三棱锥及球面，所得截面如右图所示，则此三棱锥的侧面积为

9

4

15

．

Answer 1

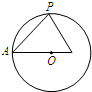
分析：将截面图转化为立体图，求三棱锥的侧面积就是求正三棱锥P-ABC中的△PAB的面积，从而得出此三棱锥的侧面积．

解答：解：如图球的截面图就是正三棱锥中的△PAD，
已知半径为

3

的球，
所以AO=PO=

3

，且PO⊥AO
所以侧棱长PA=

6

，
AD=

3

2

AO=

3 3

2

，AB=

3

2

，AB=3，
截面PAB面积是：

1

2

×AB×

PA 2-( 1 2 AB) 2

=

3

4

15

∴则此三棱锥的侧面积为

9

4

15

故答案为：

9

4

15

点评：本题考查球内接多面体以及棱锥的特征，考查空间想象能力，是中档题．