题目内容
数列{an}中,a1= ,前n项和Sn满足Sn+1-Sn=(
,前n项和Sn满足Sn+1-Sn=( )n+1(n∈)N*.
)n+1(n∈)N*.(Ⅰ)求数列{a n}的通项公式a n以及前n项和Sn
(Ⅱ)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
【答案】分析:(Ⅰ)根据an+1=Sn+1-Sn求得an+1进而根据a1求得数列{an}的通项公式,根据等比数列的求和公式求得前n项的和.
(Ⅱ)根据求得(1)的前n项和的公式,求得S1,S2,S3,进而根据等差中项的性质求得t.
解答:解:解:(Ⅰ)由Sn+1-Sn=( )n+1得
)n+1得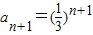 (n∈N*);
(n∈N*);
又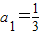 ,故
,故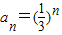 (n∈N*)
(n∈N*)
从而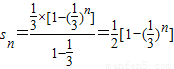 (n∈N*).
(n∈N*).
(Ⅱ)由(Ⅰ)可得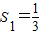 ,
,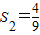 ,
,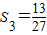 .
.
从而由S1,t(S1+S2),3(S2+S3)成等差数列可得: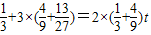 ,解得t=2.
,解得t=2.
点评:本题主要考查了等比数列的通项公式和求和公式.属基础题.
(Ⅱ)根据求得(1)的前n项和的公式,求得S1,S2,S3,进而根据等差中项的性质求得t.
解答:解:解:(Ⅰ)由Sn+1-Sn=(
 )n+1得
)n+1得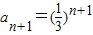 (n∈N*);
(n∈N*);又
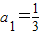 ,故
,故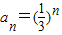 (n∈N*)
(n∈N*)从而
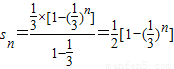 (n∈N*).
(n∈N*).(Ⅱ)由(Ⅰ)可得
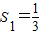 ,
,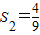 ,
,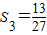 .
.从而由S1,t(S1+S2),3(S2+S3)成等差数列可得:
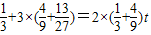 ,解得t=2.
,解得t=2.点评:本题主要考查了等比数列的通项公式和求和公式.属基础题.

练习册系列答案
相关题目
数列{an}中,a1=
,an+an+1=
,n∈N*,则
(a1+a2+…+an)等于( )
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|