Question

【题目】在公差不为零的等差数列{an}中，a2=1，a2、a4、a8成等比数列．
（1）求数列{an}的通项公式an；
（2）设数列{an}的前n项和为Sn ， 记bn= ．Tn=b1+b2+…+bn ， 求Tn ．

Answer 1

【答案】
（1）解：公差d不为零的等差数列{an}中，满足a2=1，a2、a4、a8成等比数列．

∴a1+d=1， =a2a8即（1+2d）2=1×（1+6d），

解得 ．

∴an= =

（2）解：由（1）可得：Sn= = ．

∴bn= = =4 ．

∴Tn=b1+b2+…+bn= +…+ ]=4 =

【解析】（1）公差d不为零的等差数列{an}中，满足a2=1，a2、a4、a8成等比数列．可得a1+d=1， =a2a8即（1+2d）2=1×（1+6d），解出即可得出．（2）由（1）可得：Sn= ．可得bn= = =4 ．利用“裂项求和”即可得出．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系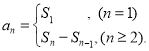，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．