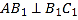题目内容
【题目】如图，甲、乙两个企业的用电负荷量
关于投产持续时间
（单位：小时）的关系
均近似地满足函数
．
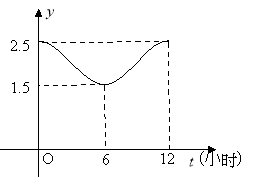
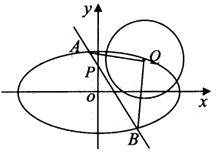
（1）根据图象，求函数
的解析式；
（2）为使任意时刻两企业用电负荷量之和不超过
，现采用错峰用电的方式，让企业乙比企业甲推迟
小时投产，求的最小值．
【答案】（1）
（2）4
【解析】
试题（1）由图象可得：
，周期
，
，求得
的解析式；（2）设乙投产持续时间为
小时，则甲的投产持续时间为（
）小时，企业乙用电负荷量随持续时间变化的关系式为：
；同理，企业甲用电负荷量变化关系式为：
； 两企业用电负荷量之和为
，依题意，有
恒成立，求得m最值 ；
试题解析：（Ⅰ）由图象可得：，
解得
周期，，
，
又
过点
，
且
，
，
（Ⅱ）设乙投产持续时间为小时，则甲的投产持续时间为（）小时
由诱导公式，企业乙用电负荷量随持续时间变化的关系式为：；
同理，企业甲用电负荷量变化关系式为：；
两企业用电负荷量之和
；
依题意，有
恒成立，
即
恒成立，
展开有：
恒成立，------10分
（其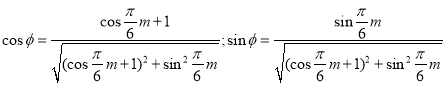
）；
，
整理得到：
，
依据余弦函数图像得：
，
即
，取
得：
∴
的最小值为4．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
