题目内容
(1)判断函数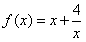 在x∈(0,+∞)上的单调性并证明你的结论;
在x∈(0,+∞)上的单调性并证明你的结论;
(2)猜想函数 在x∈(-∞,0)∪(0,+∞)上的单调性。(只需写出结论,不用证明)
在x∈(-∞,0)∪(0,+∞)上的单调性。(只需写出结论,不用证明)
(3)利用题(2)的结论,求使不等式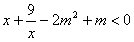 在x∈[1,5]上恒成立时的实数m的取值范围。
在x∈[1,5]上恒成立时的实数m的取值范围。
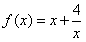 在x∈(0,+∞)上的单调性并证明你的结论;
在x∈(0,+∞)上的单调性并证明你的结论;(2)猜想函数
 在x∈(-∞,0)∪(0,+∞)上的单调性。(只需写出结论,不用证明)
在x∈(-∞,0)∪(0,+∞)上的单调性。(只需写出结论,不用证明)(3)利用题(2)的结论,求使不等式
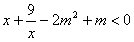 在x∈[1,5]上恒成立时的实数m的取值范围。
在x∈[1,5]上恒成立时的实数m的取值范围。 解:(1) 在(0,2]上是减函数,在[2,+∞)上是增函数。
在(0,2]上是减函数,在[2,+∞)上是增函数。
证明:设任意 ,
,
则 ,
,
又设 ,则
,则 ,∴
,∴ ;
;
∴ 在(0,2]上是减函数;
在(0,2]上是减函数;
又设 ,则
,则 ,∴
,∴ ,
,
∴ 在[2,+∞)上是增函数。
在[2,+∞)上是增函数。
(2)由(1)及f(x)是奇函数,可猜想:f(x)在 和
和 上是增函数, f(x)在
上是增函数, f(x)在 和
和 上是减函数。
上是减函数。
(3)∵ 在x∈[1,5]上恒成立,
在x∈[1,5]上恒成立,
∴ x∈[1,5]上恒成立,
x∈[1,5]上恒成立,
由(2)中结论,可知函数 在x∈[1,5]上的最大值为10,此时x=1,
在x∈[1,5]上的最大值为10,此时x=1,
要使原命题成立,当且仅当 ,
,
∴ ,解得:m<-2或
,解得:m<-2或 ,
,
∴实数m的取值范围是{m|m<-2或 }。
}。
 在(0,2]上是减函数,在[2,+∞)上是增函数。
在(0,2]上是减函数,在[2,+∞)上是增函数。证明:设任意
 ,
,则
 ,
,又设
 ,则
,则 ,∴
,∴ ;
;∴
 在(0,2]上是减函数;
在(0,2]上是减函数;又设
 ,则
,则 ,∴
,∴ ,
,∴
 在[2,+∞)上是增函数。
在[2,+∞)上是增函数。 (2)由(1)及f(x)是奇函数,可猜想:f(x)在
 和
和 上是增函数, f(x)在
上是增函数, f(x)在 和
和 上是减函数。
上是减函数。 (3)∵
 在x∈[1,5]上恒成立,
在x∈[1,5]上恒成立,∴
 x∈[1,5]上恒成立,
x∈[1,5]上恒成立,由(2)中结论,可知函数
 在x∈[1,5]上的最大值为10,此时x=1,
在x∈[1,5]上的最大值为10,此时x=1,要使原命题成立,当且仅当
 ,
,∴
 ,解得:m<-2或
,解得:m<-2或 ,
,∴实数m的取值范围是{m|m<-2或
 }。
}。
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目