题目内容

下列命题正确的是

A.
若 $数学公式$ 与 $数学公式$ 共线， $数学公式$ 与 $数学公式$ 共线，则 $数学公式$ 与 $数学公式$ 共线
B.
向量 $数学公式$ 共面就是它们所在的直线共面
C.
零向量没有确定的方向
D.
若 $数学公式$ ，则存在唯一的实数λ使得 $数学公式$

C
分析：从向量共线反例判断A，共面向量定理判断B，零向量的定义判断C，共线向量定理判断D．推出正确命题选项．
解答：若 $\text{[math]}$ 与 $\text{[math]}$ 共线， $\text{[math]}$ 与 $\text{[math]}$ 共线，则 $\text{[math]}$ 与 $\text{[math]}$ 共线，如果 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 不共线，A不正确．
向量 $\text{[math]}$ 共面就是它们所在的直线共面，这是不正确的，三个向量所在直线可以互为异面直线．
零向量没有确定的方向，满足零向量的定义．
若 $\text{[math]}$ ，则存在唯一的实数λ使得 $\text{[math]}$ ，不正确，因为 $\text{[math]}$ ，存在这一条件．
故选C．
点评：本题考查共线向量与共面向量，考查学生基本知识掌握运算的能力．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

（08年内江市三模）下列命题正确的是

A、函数的反函数为

B、如函数为奇函数，则

C、

D、函数的最小值为

已知直线m⊥平面α,直线n

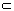平面β,则下列命题正确的是

A.若α∥β,则m⊥n B.若α⊥β,则m∥n

C.若m⊥n,则α∥β D.若n∥α,β∥α

在空间中，下列命题正确的是

A．平行于同一平面的两条直线平行 B．垂直于同一平面的两条直线平行

C．平行于同一直线的两个平面平行 D．垂直于同一平面的两个平面平行

下列命题正确的是

A．若直线a∥平面，直线b直线a，b平面，则

B．若直线a∥直线b，则a平行于过b的所有平面

C．若直线a直线b，a平面，b平面，则

D．过平面处一点有且只有一个平面与已知平面垂直

下列命题正确的是 ( )

A．若则 B．若，则

C．若则 D．若则