题目内容
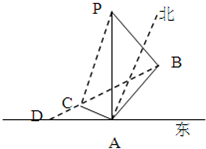 “神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为B,C,D).当返回舱距地面1万米的P点时(假定以后垂直下落,并在A点着陆),C救援中心测得飞船位于其南偏东60°方向,仰角为60°,B救援中心测得飞船位于其南偏西30°方向,仰角为30°.D救援中心测得着陆点A位于其正东方向.
“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为B,C,D).当返回舱距地面1万米的P点时(假定以后垂直下落,并在A点着陆),C救援中心测得飞船位于其南偏东60°方向,仰角为60°,B救援中心测得飞船位于其南偏西30°方向,仰角为30°.D救援中心测得着陆点A位于其正东方向.(1)求B,C两救援中心间的距离;
(2)D救援中心与着陆点A间的距离.
分析:(1)根据题意可知△PAC,△PAB均为直角三角形,进而分别在两个三角形中利用其中的一角和一边求得AC和AB,最后利用勾股定理求得BC.
(2)先利用同角三角函数的基本关系求得cos∠ACD,进而利用sin∠ADC=sin(30°+∠ACD)借助两角和公式求得sin∠ADC,最后利用正弦定理求得AD.
(2)先利用同角三角函数的基本关系求得cos∠ACD,进而利用sin∠ADC=sin(30°+∠ACD)借助两角和公式求得sin∠ADC,最后利用正弦定理求得AD.
解答:解:(1)由题意知PA⊥AC,PA⊥AB,则△PAC,△PAB均为直角三角形
在Rt△PAC中,PA=1,∠PCA=60°,解得AC=
在Rt△PAB中,PA=1,∠PBA=30°,解得AB=
又∠CAB=90°,BC=
=
万米
(2)sin∠ACD=sin∠ACB=
,cos∠ACD=-
,
又∠CAD=30°,所以sin∠ADC=sin(30°+∠ACD)=
在△ADC中,由正弦定理,
=
AD=
=
万米
在Rt△PAC中,PA=1,∠PCA=60°,解得AC=
| ||
| 3 |
在Rt△PAB中,PA=1,∠PBA=30°,解得AB=
| 3 |
又∠CAB=90°,BC=
| AC2+BC2 |
| ||
| 3 |
(2)sin∠ACD=sin∠ACB=
| 3 | ||
|
| 1 | ||
|
又∠CAD=30°,所以sin∠ADC=sin(30°+∠ACD)=
3
| ||
2
|
在△ADC中,由正弦定理,
| AC |
| sin∠ADC |
| AD |
| sin∠ACD |
AD=
| AC•sin∠ACD |
| sin∠ADC |
9+
| ||
| 13 |
点评:本题主要考查了解三角形的实际应用.解此类题的要点是建立适当的三角函数模型,利用三角函数的基本公式和定理进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
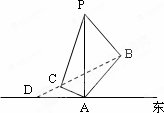
 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为 ).当返回舱距地面1万米的
).当返回舱距地面1万米的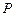 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在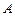 点着陆),
点着陆), 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东 方向,仰角为
方向,仰角为 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西 方向,仰角为
方向,仰角为 救援中心测得着陆点
救援中心测得着陆点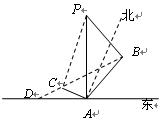

 两救援中心间的距离;
两救援中心间的距离; 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为 ).当返回舱距地面1万米的
).当返回舱距地面1万米的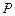 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在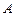 点着陆),
点着陆), 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东 方向,仰角为
方向,仰角为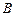 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西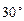 方向,仰角为
方向,仰角为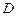 救援中心测得着陆点
救援中心测得着陆点
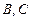
 两救援中心间的距离;
两救援中心间的距离;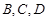 ).当返回舱距地面1万米的
).当返回舱距地面1万米的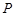 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在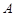 点着陆),
点着陆),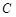 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东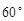 方向,仰角为
方向,仰角为 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西 方向,仰角为
方向,仰角为 救援中心测得着陆点
救援中心测得着陆点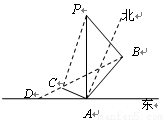
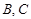 两救援中心间的距离;
两救援中心间的距离;