题目内容
设P(x0,y0)是双曲线 =1上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R两点,则平行四边形OQPR的面积为…( )
=1上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R两点,则平行四边形OQPR的面积为…( )
 =1上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R两点,则平行四边形OQPR的面积为…( )
=1上任一点,过P作双曲线两条渐近线的平行线分别交另一条渐近线于Q、R两点,则平行四边形OQPR的面积为…( )| A.b | B.2ab | C.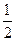 ab ab | D.4ab |
C
直线PQ的方程为y-y0=- (x-x0),直线OQ的方程为y=
(x-x0),直线OQ的方程为y= x,联立解得xQ=
x,联立解得xQ= (ay0+bx0).
(ay0+bx0).
又P到渐近线OQ的距离d= ,又tan∠xOQ=
,又tan∠xOQ= ,∴cos∠xOQ=
,∴cos∠xOQ= .
.
∴S OQPR=2S△OPQ=|OQ|·d=
OQPR=2S△OPQ=|OQ|·d= =
= ·
· |ay0+bx0|·
|ay0+bx0|· =
=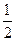 ab.
ab.
 (x-x0),直线OQ的方程为y=
(x-x0),直线OQ的方程为y= x,联立解得xQ=
x,联立解得xQ= (ay0+bx0).
(ay0+bx0).又P到渐近线OQ的距离d=
 ,又tan∠xOQ=
,又tan∠xOQ= ,∴cos∠xOQ=
,∴cos∠xOQ= .
.∴S
 OQPR=2S△OPQ=|OQ|·d=
OQPR=2S△OPQ=|OQ|·d= =
= ·
· |ay0+bx0|·
|ay0+bx0|· =
=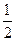 ab.
ab.
练习册系列答案
相关题目
 =1表示双曲线的____________条件.
=1表示双曲线的____________条件.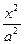 -
-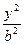 =1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )
=1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )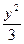 =1的左焦点F1作倾斜角为
=1的左焦点F1作倾斜角为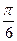 的弦AB,求:
的弦AB,求: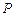 的轨迹是曲线
的轨迹是曲线 ,满足点
,满足点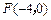 的距离与它到直线
的距离与它到直线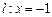 的距离
的距离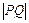 之比为常数,又点
之比为常数,又点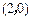 在曲线
在曲线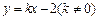 与曲线
与曲线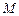 和
和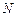 ,求实数
,求实数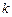 的取值范围.
的取值范围.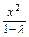 -
-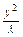 =1(0<
=1(0<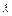 <1)的右焦点为B,过点B作直线交双曲线C的右支于M、N两点,试确定
<1)的右焦点为B,过点B作直线交双曲线C的右支于M、N两点,试确定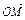 ·
·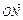 =0,其中点O为坐标原点.
=0,其中点O为坐标原点.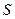 的两条渐进线过坐标原点,且与以点
的两条渐进线过坐标原点,且与以点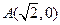 为圆心,
为圆心,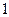 为半径的圆相且,双曲线的一个顶点
为半径的圆相且,双曲线的一个顶点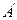 与点
与点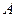 关于直线
关于直线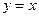 对称,设直线
对称,设直线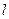 过点
过点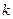 。
。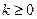 时,若双曲线
时,若双曲线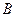 到直线
到直线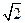 ,求斜率
,求斜率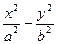 =1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )
=1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )